设x.y满足不等式$\left\{\begin{array}{l}y≤2\\ x+y≥1\\ x-y≤1\end{array}$.若目标函数z=2x+y的最大值为M.则式子2${\;}^{lo{g} {2}M}$+log2M的值为11．题目和参考答案——青夏教育精英家教网—

题目内容

15．设x，y满足不等式$\left\{\begin{array}{l}y≤2\\ x+y≥1\\ x-y≤1\end{array}$，若目标函数z=2x+y的最大值为M，则式子2${\;}^{lo{g}_{2}M}$+log₂M的值为11．

分析由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数求得M，再由对数的运算性质得答案．

解答解：由约束条件$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{x-y≤1}\end{array}\right.$作出可行域如图：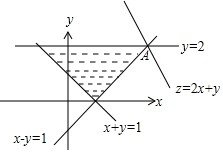

联立$\left\{\begin{array}{l}{y=2}\\{x-y=1}\end{array}\right.$，解得A（3，2），
化目标函数z=2x+y为y=-2x+z，由图可知，当直线y=-2x+z过点A时，直线在y轴上的截距最大，
z有最大值M=8．
∴${2}^{lo{g}_{2}M}+lo{g}_{2}M={2}^{lo{g}_{2}8}+lo{g}_{2}8$=8+3=11．
故答案为：11．

点评本题考查极大的线性规划，考查数形结合的解题思想方法，是中档题．

练习册系列答案

	A．	f（x）在$（-\frac{π}{4}，\frac{π}{6}）$单调递增		B．	f（x）在$（\frac{π}{4}，\frac{3}{4}π）$单调递增
	C．	f（x）在$（-\frac{π}{4}，\frac{π}{6}）$单调递减		D．	f（x）在$（\frac{π}{4}，\frac{3}{4}π）$单调递减

6．在△ABC中，c=3$\sqrt{3}$，b=3，B=30°，此三角形的解的情况是（　　）

3．已知随机变量X～N（10，2²），定义函数Φ（k）=P（X≤k），则Φ（12）-Φ（6）=0.8185．

10．已知函数f（x）=2sin（2x-$\frac{π}{6}$）-1，下面结论中错误的是（　　）

	A．	函数f（x）的最小正周期为π
	B．	函数f（x）图象关于直线x=$\frac{π}{3}$对称
	C．	函数f（x）的图象可由g（x）=2sin2x-1的图象向右平移$\frac{π}{6}$个单位得到
	D．	函数f（x）在区间$[0，\frac{π}{4}]$上是增函数

20．

如图，等腰直角△ABC中，AB=AC=1，在边AB、AC上分别取D、E两点，沿线段DE折叠，顶点A恰好落在边BC上，则AD长度的最小值为$\sqrt{2}$-1．．