题目内容
已知函数f(x)=x2+a|lnx-1|,其中a∈R.
(Ⅰ)当a=-2时,求函数f(x)在[1,e]上的最小值;
(Ⅱ)当a>0时,不等式f(x)≥
a+
在[1,+∞)上成立,求a的取值范围.
(Ⅰ)当a=-2时,求函数f(x)在[1,e]上的最小值;
(Ⅱ)当a>0时,不等式f(x)≥
| 2e-3 |
| 2e-2 |
| 2e |
| 2e-2 |
考点:函数的最值及其几何意义,分段函数的应用
专题:
分析:(Ⅰ)a=2带入原函数,根据x的取值得出函数f(x),由导数的取值判断f(x)的单调性,根据单调性求其最值.
(Ⅱ)a>0时,对于任意x∈[1,+∞)都有原不等式成立,所以只需求f(x)在[1,+∞上的最小值,让最小值满足原不等式即可.
(Ⅱ)a>0时,对于任意x∈[1,+∞)都有原不等式成立,所以只需求f(x)在[1,+∞上的最小值,让最小值满足原不等式即可.
解答:
解:(Ⅰ)由题知:a=-2,x∈[1,e]时,f(x)=x2-2(1-lnx)=x2+2lnx-2;
所以′f′(x)=2x+
>0;
所以f(x)在[1,e]上是增函数;
所以f(x)在[1,e]上的最小值是f(1)=-1.
(Ⅱ)由题知:只要求出f(x)的最小值即可.(1)当x∈[1,e)时:f(x)=x2-alnx+a;
′f′(x)=2x-
=
所以:①
≤1,即0<a≤2时,在(1,e)上f′(x)>0;所以f(x)在[1,e)上是增函数,所以fmin(x)=f(1)=a+1.所以a+1≥
a+
,解得a≥2,所以a=2.
②当1<
<e,即2<a<2e2时:在(1,
)上f′(x)<0,所以f(x)在(1,
)上是减函数;在(
,e)上f(x)′>0,所以f(x)在(
,e)上是增函数;所以x=
时,fmin(x)=
-
ln
,所以
-
ln
≥
a+
,变成ea-(e-1)aln
≥0,令y=ea-(e-1)aln
,a当变量,则y′=2-e-(e-1)ln
该函数在(2,2e2)上是减函数,所以这个函数最大值为2-e<0,所以函数y=ea-(e-a)aln
在(2,2e2)是减函数,所以ymax=2e,解ea-(e-1)aln
=0得a=2e
,所以对于任意a∈(2e
,2e),ea-(e-1)aln
≥0恒成立;
③当
≥e,即a≥2e2时,在(1,e)上f′(x)<0,所以f(x)在(1,e)上是减函数,所以fmin(x)=f(e)=e2,所以e2≥
a+
,解得a∈(0,
]
(2)当x∈[e,+∞)时:f(x)=x2+alnx-a,所以f′(x)=2x+
>0,所以f(x)在[e,+∞)上是增函数,所以fmin(x)=f(e)=e2.综上得:a的取值范围是{a/a=2,或2e
<a<2e,或0<a≤
}
所以′f′(x)=2x+
| 2 |
| x |
所以f(x)在[1,e]上是增函数;
所以f(x)在[1,e]上的最小值是f(1)=-1.
(Ⅱ)由题知:只要求出f(x)的最小值即可.(1)当x∈[1,e)时:f(x)=x2-alnx+a;
′f′(x)=2x-
| a |
| x |
2(x+
| ||||||||
| x |
|
| 2e-3 |
| 2e-2 |
| 2e |
| 2e-2 |
②当1<
|
|
|
|
|
|
| 3a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 3a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 2e-3 |
| 2e-2 |
| 2e |
| 2e-2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| e |
| e-1 |
| e |
| e-1 |
| a |
| 2 |
③当
|
| 2e-3 |
| 2e-2 |
| 2e |
| 2e-2 |
| 2e3-2e2-2e |
| 2e-3 |
(2)当x∈[e,+∞)时:f(x)=x2+alnx-a,所以f′(x)=2x+
| a |
| x |
| e |
| e-1 |
| 2e3-2e2-2e |
| 2e-3 |
点评:注意运用:1.导数与函数单调性的关系:导数大于0时,在对应区间上是增函数;导数小于0时,在相应区间上是件函数;
2.单调性与最值得关系:单调函数在端点处取得最值.
2.单调性与最值得关系:单调函数在端点处取得最值.

练习册系列答案
相关题目
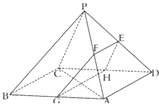 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2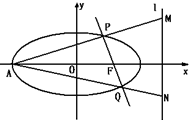 如图,已知椭圆C:
如图,已知椭圆C: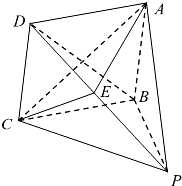 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,AC与BD交于O点,E为PC的中点,AD=CD=1,PD=2,DB=2
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,AC与BD交于O点,E为PC的中点,AD=CD=1,PD=2,DB=2