题目内容
已知函数f(x)=x-alnx+
(a∈R).
(1)求函数f(x)的单调区间;
(2)若f(x)在区间[1,e]上存在一个零点,求a的取值范围.
| 1+a |
| x |
(1)求函数f(x)的单调区间;
(2)若f(x)在区间[1,e]上存在一个零点,求a的取值范围.
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:(1)先求出函数的导数,再通过讨论a的范围,从而求出其单调区间,(2)f(x)在区间[1,e]上存在一个零点等价于f(x)在区间[1,e]的最小值不大于0,再由①若1+a≥e,②当1+a≤1,③当1<1+a<e,综合得出结论.
解答:
解:(1)函数f(x)的定义域为(0,+∞).
∴f′(x)=1-
-
=
=
,
由定义域可知x+1>0.
①当a+1>0,即a>-1时,
由f'(x)>0得x>1+a;由f'(x)<0得x<1+a.
所以f(x)的增区间为(1+a,+∞),减区间为(0,1+a).
②当1+a≤0,即a≤-1时,易见f'(x)>0.
所以f(x)的增区间为(0,+∞).
(2)f(x)在区间[1,e]上存在一个零点等价于f(x)在区间[1,e]的最小值不大于0.
①若1+a≥e,即a≥e-1时,由(1)可知f(x)在区间[1,e]为减函数,
所以f(x)min=f(e)=e+
-a≤0,
解得a≥
因为
>e-1,所以a≥
.
②当1+a≤1,即a≤0时,f(x)在[1,e]上单调递增,
所以f(x)的最小值为f(1)=1+1+a≤0
解得a≤-2.
③当1<1+a<e,即0<a<1-e时,f(x)的最小值为f(1+a)=2+a-aln(1+a)
因为0<ln(1+a)<1,所以f(1+a)=2+a[1-ln(1+a)]>2
即此时f(x)在区间[1,e]上无零点.
综合①,②,③的讨论可知a的取值范围是(-∞, -2]∪[
, +∞].
∴f′(x)=1-
| a |
| x |
| 1+a |
| x2 |
| x2-ax-(1+a) |
| x2 |
| (x+1)[x-(1+a)] |
| x2 |
由定义域可知x+1>0.
①当a+1>0,即a>-1时,
由f'(x)>0得x>1+a;由f'(x)<0得x<1+a.
所以f(x)的增区间为(1+a,+∞),减区间为(0,1+a).
②当1+a≤0,即a≤-1时,易见f'(x)>0.
所以f(x)的增区间为(0,+∞).
(2)f(x)在区间[1,e]上存在一个零点等价于f(x)在区间[1,e]的最小值不大于0.
①若1+a≥e,即a≥e-1时,由(1)可知f(x)在区间[1,e]为减函数,
所以f(x)min=f(e)=e+
| 1+a |
| e |
解得a≥
| e2+1 |
| e-1 |
因为
| e2+1 |
| e-1 |
| e2+1 |
| e-1 |
②当1+a≤1,即a≤0时,f(x)在[1,e]上单调递增,
所以f(x)的最小值为f(1)=1+1+a≤0
解得a≤-2.
③当1<1+a<e,即0<a<1-e时,f(x)的最小值为f(1+a)=2+a-aln(1+a)
因为0<ln(1+a)<1,所以f(1+a)=2+a[1-ln(1+a)]>2
即此时f(x)在区间[1,e]上无零点.
综合①,②,③的讨论可知a的取值范围是(-∞, -2]∪[
| e2+1 |
| e-1 |
点评:本题考察了函数的单调性,导数的应用,渗透了数形结合思想,是一道综合题.

练习册系列答案
相关题目
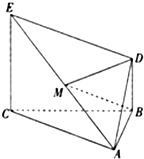 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点 如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2
如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2