题目内容
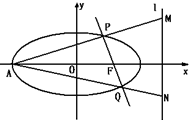 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| 4 |
| y2 |
| 3 |
(Ⅰ)当
| AP |
| AQ |
| 9 |
| 2 |
(Ⅱ)试问M,N两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)当直线PQ的斜率不存在时,推导出
•
=
不满足;当直线PQ的斜率存在时,设PQ方程为y=k(x-1)(k≠0)代入椭圆C:
+
=1,得(3+4k2)x2-8k2x+4k2-12=0,由此利用韦达定理结合已知条件能求出直线l′的方程.
(Ⅱ)AP的方程为y=
(x+2)与l的方程:x=4联立得:M(4,
),同理得N(4,
),由此能推导出M,N两点的纵坐标之积为定值-9.
| AP |
| AQ |
| 27 |
| 4 |
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)AP的方程为y=
| y1 |
| x1+2 |
| 6y1 |
| x1+2 |
| 6y2 |
| x2+2 |
解答:
解:(Ⅰ)①当直线PQ的斜率不存在时,
由F(1,0)知PQ方程为x=1
代入椭圆C:
+
=1,得P(1,
),Q(1,-
),
又A(-2,0)∴
=(3,
),
=(3,-
),
•
=
不满足…(2分)
②当直线PQ的斜率存在时,设PQ方程为y=k(x-1)(k≠0)
代入椭圆C:
+
=1,
得(3+4k2)x2-8k2x+4k2-12=0…(3分)
设P(x1,y1),Q(x2,y2),
得x1+x2=
,x1x2=
…(4分)y1y2=k2(x1-1)(x2-1)=k2(-x1-x2+x1x2+1)=
,
∴k=±
,故直线l′的方程y=±
(x-1)…(6分)
(Ⅱ)AP的方程为y=
(x+2)与l的方程:x=4联立得:M(4,
),
同理得N(4,
)…(8分)
∴yM•yN=
•
=
①k不存在时,yM•yN=
=-9…(9分)
②k存在时,yM•yN=
=-9…(12分)
∴M,N两点的纵坐标之积为定值-9…(13分)
由F(1,0)知PQ方程为x=1
代入椭圆C:
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
又A(-2,0)∴
| AP |
| 3 |
| 2 |
| AQ |
| 3 |
| 2 |
| AP |
| AQ |
| 27 |
| 4 |
②当直线PQ的斜率存在时,设PQ方程为y=k(x-1)(k≠0)
代入椭圆C:
| x2 |
| 4 |
| y2 |
| 3 |
得(3+4k2)x2-8k2x+4k2-12=0…(3分)
设P(x1,y1),Q(x2,y2),
得x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
| -9k2 |
| 3+4k2 |
|
∴k=±
| ||
| 2 |
| ||
| 2 |
(Ⅱ)AP的方程为y=
| y1 |
| x1+2 |
| 6y1 |
| x1+2 |
同理得N(4,
| 6y2 |
| x2+2 |
∴yM•yN=
| 6y1 |
| x1+2 |
| 6y2 |
| x2+2 |
| 36y1y2 |
| x1x2+2(x1+x2)+4 |
①k不存在时,yM•yN=
36•
| ||||
| 1+2(1+1)+4 |
②k存在时,yM•yN=
-
| ||||
|
∴M,N两点的纵坐标之积为定值-9…(13分)
点评:本题考查直线方程的求法,考查两点横坐标之积是否这定点的判断与求法,解题时要认真审题,注意向量的数量积的合理运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
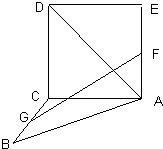 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值. 如图,在空间直角坐标系A-xyz中,已知斜四棱柱ABCD-A1B1C1D1的底面是边长为3的正方形,点B,D,B1分别在x,y,z轴上,B1A=3,P是侧棱B1B上的一点,BP=2PB1.
如图,在空间直角坐标系A-xyz中,已知斜四棱柱ABCD-A1B1C1D1的底面是边长为3的正方形,点B,D,B1分别在x,y,z轴上,B1A=3,P是侧棱B1B上的一点,BP=2PB1.