题目内容
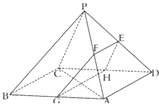 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2| 2 |
| 5 |
(Ⅰ)证明:EF∥平面ABCD;
(Ⅱ)求四棱锥P-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)由已知条件推导出EH∥PC,EF∥AD,由此能证明EF∥平面ABCD.
(Ⅱ)设AC∩BD=O,证明PO⊥平面ABCD,利用体积公式,即可求出四棱锥P-ABCD的体积.
(Ⅱ)设AC∩BD=O,证明PO⊥平面ABCD,利用体积公式,即可求出四棱锥P-ABCD的体积.
解答:
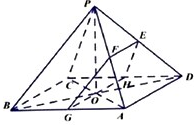 (Ⅰ)证明:∵平面EFGH∥平面PBC,
(Ⅰ)证明:∵平面EFGH∥平面PBC,
平面EFGH∩平面PCD=EH,平面PBC∩平面PCD=PC,
∴EH∥PC,又E是PD的中点,∴H是CD的中点,
同理可证F,G分别是PA、AB的中点,
∴EF∥AD,又EF不包含于平面ABCD,AD?平面ABCD,
∴EF∥平面ABCD.
(Ⅱ)解:∵底面ABCD是边长为2
的正方形,
设AC∩BD=O,则AC⊥BD,且AC=BD=4,
由侧面侧棱长为
的等腰三角形,知:
PO⊥AC,PO⊥BD,∴PO⊥平面ABCD,
在Rt△PAO中,PO=1,
∴VP-ABCD=
SABCD•PO=
•(2
)2•1=
.
 (Ⅰ)证明:∵平面EFGH∥平面PBC,
(Ⅰ)证明:∵平面EFGH∥平面PBC,平面EFGH∩平面PCD=EH,平面PBC∩平面PCD=PC,
∴EH∥PC,又E是PD的中点,∴H是CD的中点,
同理可证F,G分别是PA、AB的中点,
∴EF∥AD,又EF不包含于平面ABCD,AD?平面ABCD,
∴EF∥平面ABCD.
(Ⅱ)解:∵底面ABCD是边长为2
| 2 |
设AC∩BD=O,则AC⊥BD,且AC=BD=4,
由侧面侧棱长为
| 5 |
PO⊥AC,PO⊥BD,∴PO⊥平面ABCD,
在Rt△PAO中,PO=1,
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 8 |
| 3 |
点评:本题考查直线与平面平行的证明,考查四棱锥的体积,要求熟练掌握相应的判定定理.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
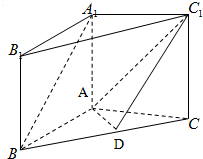 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2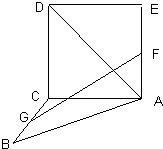 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.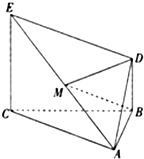 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点 如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2
如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2