题目内容
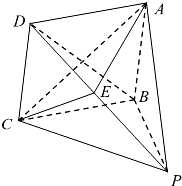 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.(l)若AC=6,BD=8,PB=3,求三棱锥A一PBC的体积;
(2)若点E是DP的中点,证明:BD⊥平面ACE.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)利用转换底面求三棱锥A一PBC的体积;
(2)设BD∩AC=O,连接OE,证明OE⊥平面ABCD,可得OE⊥BD,利用AC⊥BD,即可证明BD⊥平面ACE.
(2)设BD∩AC=O,连接OE,证明OE⊥平面ABCD,可得OE⊥BD,利用AC⊥BD,即可证明BD⊥平面ACE.
解答:
 (1)解:∵底面ABCD为菱形,
(1)解:∵底面ABCD为菱形,
∴BD与AC垂直平分,
∴S△ABC=
S菱形ABCD=
×
×6×8=12,
∵PB⊥平面ABCD,PB=3,
∴VA一PBC=VP-ABC=
×12×3=12;
(2)证明:设BD∩AC=O,连接OE,则
∵O为BD的中点,E是PD的中点,
∴OE∥PB,
∵PB⊥平面ABCD,
∴OE⊥平面ABCD,
∵BD?平面ABCD,
∴OE⊥BD,
∵AC⊥BD,AC∩OE=O,
∴BD⊥平面ACE.
 (1)解:∵底面ABCD为菱形,
(1)解:∵底面ABCD为菱形,∴BD与AC垂直平分,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵PB⊥平面ABCD,PB=3,
∴VA一PBC=VP-ABC=
| 1 |
| 3 |
(2)证明:设BD∩AC=O,连接OE,则
∵O为BD的中点,E是PD的中点,
∴OE∥PB,
∵PB⊥平面ABCD,
∴OE⊥平面ABCD,
∵BD?平面ABCD,
∴OE⊥BD,
∵AC⊥BD,AC∩OE=O,
∴BD⊥平面ACE.
点评:本题考查体积的计算,考查线面垂直,正确运用线面垂直的判定定理是关键.

练习册系列答案
相关题目
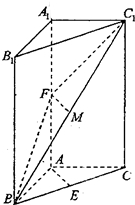 如图,在三棱柱ABC-A1B1C1中,A1A⊥面ABC,∠BAC=90°,E为BC的中点,F为A1A的中点,A1A=4,AB=AC=2.
如图,在三棱柱ABC-A1B1C1中,A1A⊥面ABC,∠BAC=90°,E为BC的中点,F为A1A的中点,A1A=4,AB=AC=2.