题目内容
平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.
考点:直线与平面垂直的判定
专题:证明题
分析:要证明PO垂直于AB、AD,只需证明PO垂直于平行四边形ABCD所在平面即可,由PA=PB=PC=PD,可以证明三角形PAC、PBD为等腰三角形,O为平行四边形ABCD的对角线的交点,因此,可以得到PO⊥AC,PO⊥BD,从而可以证明结论.
解答:
证明:连接AC、BD交与一点O,连接PO,PA、PC、PB、PD,
则由PA=PB=PC=PD,所以三角形PAC为等腰三角形,
O是AC的中点,所以PO⊥AC,同理可以证明PO⊥BD,
又AC∩BD=O,所以PO⊥平面ABCD,
而AB?平面ABCD,BD?平面ABCD,从而PO垂直于AB、AD.
则由PA=PB=PC=PD,所以三角形PAC为等腰三角形,
O是AC的中点,所以PO⊥AC,同理可以证明PO⊥BD,
又AC∩BD=O,所以PO⊥平面ABCD,
而AB?平面ABCD,BD?平面ABCD,从而PO垂直于AB、AD.
点评:本题考查线线垂直的证明,将其转化为线面垂直来证明,这也是证明线线关系、线面关系常用的方法.

练习册系列答案
相关题目
已知点P(x,y)在以原点为圆心的单位圆上运动,则点Q(x+y,xy)的轨迹是( )
| A、圆 | B、抛物线 | C、椭圆 | D、双曲线 |

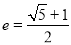 的双曲线
的双曲线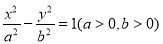 为黄金双曲线.如图是双曲线
为黄金双曲线.如图是双曲线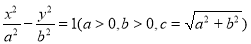 的图象,给出以下几个说法:
的图象,给出以下几个说法: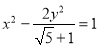 是黄金双曲线;
是黄金双曲线;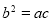 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;