题目内容
2．函数f（x）=3x2+ex-2（x＜0）与g（x）=3x2+ln（x+t）图象上存在关于y轴对称的点，则t的取值范围是（ ）| A． | （-∞，$\frac{1}{e}$） | B． | （-∞，e） | C． | （-e，$\frac{1}{e}$） | D． | （-$\frac{1}{e}$，e） |
分析 若函数f（x）=3x2+ex-2（x＜0）与g（x）=3x2+ln（x+t）的图象上存在关于y轴对称的点，则函数f（x）=3x2+ex-2（x＜0）关于y对称后的图象与g（x）=3x2+ln（x+t）的图象有交点，进而可得实数t的取值范围．
解答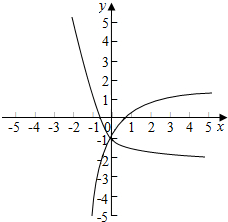 
解：若函数f（x）=3x2+ex-2（x＜0）与g（x）=3x2+ln（x+t）的图象上存在关于y轴对称的点，
则函数f（x）=3x2+ex-2（x＜0）关于y对称后的图象与g（x）=3x2+ln（x+t）的图象有交点，
即2x2+e-x=2x2+ln（x+t）+2有正根，
即e-x=ln（x+t）+2有正根，
即e-x-2=ln（x+t）有正根，
即函数y=e-x-2和y=ln（x+t）的图象在y轴右侧有交点，
如下图所示：
由lnt=-1得：t=$\frac{1}{e}$得：满足条件的实数m的取值范围是（-∞，$\frac{1}{e}$），
故选：A．
点评 本题主要考察函数图象的对称变换，函数交点个数及位置的判定，属于中档题．
练习册系列答案
相关题目
18．若集合M={y|y=x4，x∈（-1，0）}，集合$N=\left\{{x|y=ln\frac{x}{x-1}}\right\}$，则下列各式中正确的是（ ）
| A． | M?N | B． | N?M | C． | M∩N=ϕ | D． | M=N |
19．已知$cos（{\frac{π}{4}-α}）=\frac{4}{5}$，则sin2α=（ ）
| A． | $\frac{24}{25}$ | B． | $\frac{7}{25}$ | C． | $±\frac{24}{25}$ | D． | $±\frac{7}{25}$ |
16．在（1+x）+（1+x）2+（1+x）3+…+（1+x）11的展开式中，x2的系数是（ ）
| A． | 55 | B． | 66 | C． | 165 | D． | 220 |
3．某印刷厂为了研究印刷单册书籍的成本y（单位：元）与印刷册数x（单位：千册）之间的关系，在印制某种书籍时进行了统计，相关数据见下表：
根据以上数据，技术人员分别借助甲、乙两种不同的回归模型，得到两个回归方程，方程甲：${\stackrel{∧}{y}}^{（1）}$=$\frac{4}{x}+1.1$，方程乙：$\stackrel{{∧}^{（2）}}{y}$=$\frac{6.4}{x^2}+1.6$．
（1）为了评价两种模型的拟合效果，完成以下任务．
①完成下表（计算结果精确到0.1）；
②分别计算模型甲与模型乙的残差平方和Q1及Q2，并通过比较Q1，Q2的大小，判断哪个模型拟合效果更好．
（2）该书上市之后，受到广大读者热烈欢迎，不久便全部售罄，于是印刷厂决定进行二次印刷．根据市场调查，新需求量为8千册（概率0.8）或10千册（概率0.2），若印刷厂以每册5元的价格将书籍出售给订货商，问印刷厂二次印刷8千册还是10千册能获得更多利润？（按（1）中拟合效果较好的模型计算印刷单册书的成本）
| 印刷册数 （千册） | 2 | 3 | 4 | 5 | 8 |
| 单册成本 （元） | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
（1）为了评价两种模型的拟合效果，完成以下任务．
①完成下表（计算结果精确到0.1）；
| 印刷册数x（千册） | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y（元） | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值${\stackrel{∧}{{y}_{i}}}^{（1）}$ | 2.4 | 2.1 | 1.6 | ||
| 残差${\stackrel{∧}{{e}_{i}}}^{（1）}$ | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值 ${\stackrel{∧}{{y}_{i}}}^{（2）}$ | 2.3 | 2 | 1.9 | ||
| 残差 ${\stackrel{∧}{{e}_{i}}}^{（2）}$ | 0.1 | 0 | 0 | |||
（2）该书上市之后，受到广大读者热烈欢迎，不久便全部售罄，于是印刷厂决定进行二次印刷．根据市场调查，新需求量为8千册（概率0.8）或10千册（概率0.2），若印刷厂以每册5元的价格将书籍出售给订货商，问印刷厂二次印刷8千册还是10千册能获得更多利润？（按（1）中拟合效果较好的模型计算印刷单册书的成本）