题目内容
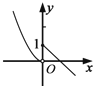
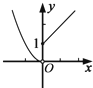
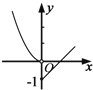
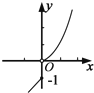
8.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )| A. | f(x)=x3 | B. | f(x)=lgx | C. | $f(x)={({\frac{1}{2}})^x}$ | D. | f(x)=3x |
分析 可先设f(x)为指数函数,并给出证明,再根据指数函数单调性的要求,得出D选项符合题意.
解答 解:指数函数满足条件“f(x+y)=f(x)f(y)”,验证如下:
设f(x)=ax,则f(x+y)=ax+y,
而f(x)f(y)=ax•ay=ax+y,
所以,f(x+y)=f(x)f(y),
再根据题意,要使f(x)单调递增,只需满足a>1即可,
参考各选项可知,f(x)=3x,即为指数函数,又为增函数,
故答案为:D.
点评 本题主要考查了指数函数的图象与性质,以及同底指数幂的运算性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.某校高三年级共1500人,在某次数学测验后分析学生试卷情况,需从中抽取一个容量为500的样本,按分层抽样,120分以上抽取100人,90~120分抽取250人,则该次测验中90分以下的人数是( )
| A. | 600 | B. | 450 | C. | 300 | D. | 150 |
19.在锐角△ABC中,内角A,B,C的对边分别为a,b,c,若sin2C-cos2C=$\frac{1}{2}$,则下列各式正确的是( )
| A. | a+b=2c | B. | a+b≤2c | C. | a+b<2c | D. | a+b≥2c |
17.已知定义在R上的奇函数f(x),当x>0时,f(x)=-x2-2ax-4.若函数f(x)有5个零点,则实数a的取值范围是( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (-2,2) |
20.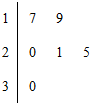 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
( )
 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 ( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |