题目内容
18．某校高三年级共1500人，在某次数学测验后分析学生试卷情况，需从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，则该次测验中90分以下的人数是（ ）| A． | 600 | B． | 450 | C． | 300 | D． | 150 |
分析 根据从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，即可得出结论．
解答 解：∵从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，
∴该次测验中90分以下抽取的人数是500-100-250=150．
∴该次测验中90分以下的人数是150．
即抽样比k=$\frac{150}{500}$，
则该次测验中90分以下的人数是1500×$\frac{150}{500}$=450．
故选：B．
点评 本题是考查分层抽样的定义，考查学生的计算能力，比较基础．
练习册系列答案
期末集结号系列答案
相关题目
8．执行如图所示的程序框图，输出$s=\frac{2015}{2016}$．那么判断框内应填（ ）
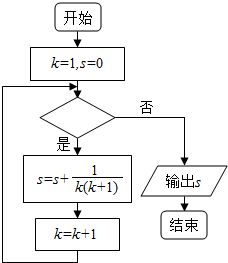
| A． | k≤2015 | B． | k≤2016 | C． | k≥2015 | D． | k≥2016 |
9．
给出以下命题：
（1）函数f（x）=$\sqrt{{x}^{2}}$与函数g（x）=|x|是同一个函数；
（2）函数f（x）=ax+1（a＞0且a≠1）的图象恒过定点（0，1）；
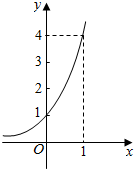
（3）设指数函数f（x）的图象如图所示，若关于x的方程f（x）=$\frac{m-1}{m+1}$有负数根，则实数m的取值范围是（1，+∞）；
（4）若f（x）=$\left\{\begin{array}{l}{{2}^{x}+t（x≥0）}\\{g（x）（x＜0）}\end{array}\right.$为奇函数，则f（f（-2））=-7；
（5）设集合M={m|函数f（x）=x2-mx+2m的零点为整数，m∈R}，则M的所有元素之和为15．
其中所有正确命题的序号为（ ）
给出以下命题：（1）函数f（x）=$\sqrt{{x}^{2}}$与函数g（x）=|x|是同一个函数；
（2）函数f（x）=ax+1（a＞0且a≠1）的图象恒过定点（0，1）；
（3）设指数函数f（x）的图象如图所示，若关于x的方程f（x）=$\frac{m-1}{m+1}$有负数根，则实数m的取值范围是（1，+∞）；
（4）若f（x）=$\left\{\begin{array}{l}{{2}^{x}+t（x≥0）}\\{g（x）（x＜0）}\end{array}\right.$为奇函数，则f（f（-2））=-7；
（5）设集合M={m|函数f（x）=x2-mx+2m的零点为整数，m∈R}，则M的所有元素之和为15．
其中所有正确命题的序号为（ ）
| A． | （1）（2）（3） | B． | （1）（3）（5） | C． | （2）（4）（5） | D． | （1）（3）（4） |
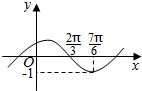已知函数f（x）=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$≤φ≤$\frac{π}{2}$）的图象如图所示，若函数g（x）=3[f（x）]3-4f（x）+m在x$∈[-\frac{π}{2}，\frac{π}{2}]$上有4个不同的零点，则实数m的取值范围是[$\frac{13}{8}$，$\frac{16}{9}$]．
8．下列函数中，满足“f（x+y）=f（x）f（y）”的单调递增函数是（ ）
| A． | f（x）=x3 | B． | f（x）=lgx | C． | $f（x）={（{\frac{1}{2}}）^x}$ | D． | f（x）=3x |