题目内容
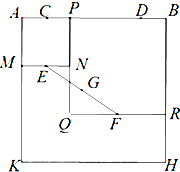 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为考点:轨迹方程
专题:综合题
分析:设KH的中点为S,连接PE,PF,SE,SF,PS,由三角形相似结合E为MN的中点,S为KH的中点可得A,E,S共线,F为QR的中点,S为KH的中点得B,F,S共线,再由三角形相似得到ES∥PF,PE∥FS,结合G为EF的中点可得G为PS的中点,即G的轨迹为△CSD的中位线,由三角形的中位线长是底边的一半得答案.
解答:
解:如图,

设KH的中点为S,连接PE,PF,SE,SF,PS,
∵E为MN的中点,S为KH的中点,∴A,E,S共线,
F为QR的中点,S为KH的中点,∴BFS共线,
由△AME∽△PQF,得∠SAP=∠FPB,∴ES∥PF,
△PNE∽△BRF,得∠EPA=∠FBP,∴PE∥FS,
则四边形PESF为平行四边形,则G为PS的中点,
∴G的轨迹为△CSD的中位线,
∵CD=AB-AC-BD=6-1-1=4,∴点G移动的路径长为
×4=2.
故答案为:2.

设KH的中点为S,连接PE,PF,SE,SF,PS,
∵E为MN的中点,S为KH的中点,∴A,E,S共线,
F为QR的中点,S为KH的中点,∴BFS共线,
由△AME∽△PQF,得∠SAP=∠FPB,∴ES∥PF,
△PNE∽△BRF,得∠EPA=∠FBP,∴PE∥FS,
则四边形PESF为平行四边形,则G为PS的中点,
∴G的轨迹为△CSD的中位线,
∵CD=AB-AC-BD=6-1-1=4,∴点G移动的路径长为
| 1 |
| 2 |
故答案为:2.
点评:本题考查了轨迹方程,考查了三角形的中位线知识,考查了三角形相似及动点的轨迹,是中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
函数y=(2a2-3a+2)ax是指数函数,则a的取值范围是( )
| A、a>0,a≠1 | ||
| B、0<a<1 | ||
C、a=
| ||
D、
|
若双曲线的标准方程为
-
=1,则它的渐近线方程为( )
| x2 |
| 8 |
| y2 |
| 4 |
A、x±
| ||
B、
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
 某空间几何体的三视图如图所示(单位:cm),则该几何体的体积V=
某空间几何体的三视图如图所示(单位:cm),则该几何体的体积V= 已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x,
已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x,