Question

正三棱锥的高为1，底面边长为2

6

．
（1）求棱锥的全面积和体积；
（2）若正三棱锥内有一个球与四个面相切，求球的表面积．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）过点P作PD⊥平面ABC于D，连结并延长AD交BC于E，连结PE，△ABC是正三角形，AE是BC边上的高和中线，D为△ABC的中心．由此能求出棱锥的全面积和体积．
（2）设球的半径为r，以球心O为顶点，棱锥的四个面为底面把正三棱锥分割为四个小棱锥，由此能求出球的表面积．

解答： 解：（1）如图，过点P作PD⊥平面ABC于D，
连结并延长AD交BC于E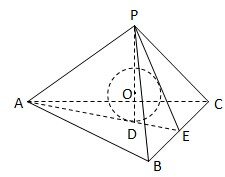，连结PE，△ABC是正三角形，
∴AE是BC边上的高和中线，D为△ABC的中心．
∵AB=2

6

，
∴S△ABC=

3

4

×(2

6

)2=6

3

，
DE=

1

3

×

3

2

AB=

2

，PE=

12+( 2 )2

=

3

．
S△PAB=S△PBC=

S

△PCA

=

1

2

×(2

6

)×

3

=3

2

．
∴S全=S侧+S底=3S△PAB+S△ABC=9

2

+6

3

，
∵BD=1，∴VP-ABC=

1

3

•S△ABC•BD=2

3

．
（2）设球的半径为r，以球心O为顶点，
棱锥的四个面为底面把正三棱锥分割为四个小棱锥，
则V1+V2+V3+V4=

1

3

r•S全=VP-ABC，
∴r=

3VP-ABC

S全

=

6 3

9 2 +6 3

=

6

-2
∴S球=4πr2=4π(

6

-2)2．

点评：本题考查棱锥的全面积和体积的求法，考查球的表面积的求法，解题时要认真审题，注意空间思维能力的培养．