Question

已知x、y满足

1≤x+y≤4 -2≤x-y≤2

目标函数Z=ax+by（a＞0，b＞0）．
（1）若a=2，b=1，求Z的最大值与最小值；
（2）若Z的最大值为6，求

6

a

+

2

b

的最小值．

Answer 1

考点：简单线性规划

专题：计算题,作图题,综合题,不等式的解法及应用

分析：（1）由题意作出其平面区域，将z=2x+y化为y=-2x+z，z相当于直线y=-2x+z的纵截距，由几何意义可得；（2）讨论Z取得最大值时的点，并令最大值为6，求

6

a

+

2

b

的最小值．

解答： 解：（1）其平面区域如下图：

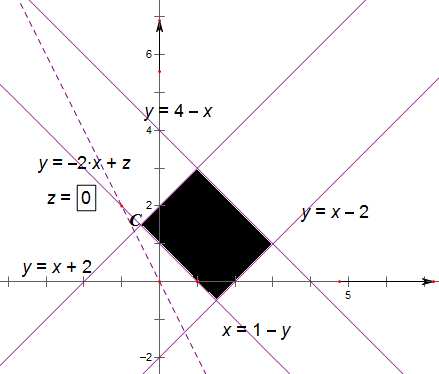
由a=2，b=1，目标函数Z=2x+y可化为y=-2x+Z，Z相当于直线y=-2x+z的纵截距，
由图可知，当x=3，y=1时有最大值，
Z_max=2×3+1=7，
当x=-0.5，y=1.5时，有最小值，
Z_max=2×（-0.5）+1.5=

1

2

．
（2）由图可知，当a＜b时，目标函数Z=ax+by的最大值在（1，3）时取得，
即a+3b=6，
则

6

a

+

2

b

=

a+3b

a

+

a+3b

b

×

1

3

=3（

b

a

+

a

9b

）+2，
∵0＜a＜b，∴

b

a

＞1，
又∵y=3（x+

1

9x

）+2在[1，+∞）上是增函数，
∴3（

b

a

+

a

9b

）+2＞3（1+

1

9

）+2=5+

1

3

=

16

3

，
当a≥b时，目标函数Z=ax+by的最大值在（3，1）时取得，
即3a+b=6，
则

6

a

+

2

b

=3+

1

3

+

b

a

+

a

b

≥

16

3

，
综上所述，

6

a

+

2

b

的最小值为：

16

3

．

点评：本题考查了简单线性规划，作图要细致认真，同时考查了最值问题，用到函数的单调性与基本不等式，属于中档题．