题目内容
已知θ是三角形中的最小角，则sin（θ+
）的取值范围是（ ）
| π |
| 3 |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由三角形的知识可得θ的范围，再求出θ+
的范围，由正弦函数的性质可得结论．
| π |
| 3 |
解答：
解：∵θ是三角形中的最小角，∴0＜θ≤
，
则
＜θ+
≤
，
∴
≤sin（θ+
）≤1，
即sin（θ+
）的取值范围是[
，1]，
故选：B．
| π |
| 3 |
则
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴
| ||
| 2 |
| π |
| 3 |
即sin（θ+
| π |
| 3 |
| ||
| 2 |
故选：B．
点评：本题考查三角函数的取值范围，以及正弦函数的性质，求出θ的范围是解决问题的关键，属基础题．
练习册系列答案
相关题目
否定：“自然数a，b，c中恰有一个偶数”时正确的反设为（ ）
| A、a，b，c都是偶数 |
| B、a，b，c都是奇数 |
| C、a，b，c中至少有两个偶数 |
| D、a，b，c中都是奇数或至少有两个偶数 |
极坐标方程4ρsin2
=5表示的曲线为（ ）
| θ |
| 2 |
| A、直线 | B、圆 | C、椭圆 | D、抛物线 |
函数y=log
（x2-ax+3）在[1，2]上恒为正数，则a的取值范围是（ ）
| 1 |
| 3 |
A、2
| ||||
B、2
| ||||
C、3＜a＜
| ||||
D、3＜a＜2
|
用秦九韶算法求多项式f（x）=7x6+6x5+3x2+2当x=4的值时，第一步算的是（ ）
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
下列命题是假命题的是（ ）
| A、若x2+y2=0，则x=y=0 |
| B、若a+b是偶数，则a，b都是偶数 |
| C、矩形的对角线相等 |
| D、余弦函数是周期函数 |
已知在二面角α-l-β的α面上有Rt△ABC，斜边BC在l上，A在β面上的射影为D，∠ABD为θ1，∠ACD为θ2，二面角α-l-β为θ．请问以下条件哪一个成立（ ）
| A、sin2θ=sin2θ1+sin2θ2 |
| B、cos2θ=cos2θ1+cos2θ2 |
| C、tan2θ=tan2θ1+tan2θ2 |
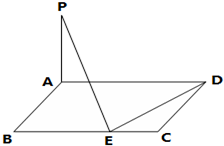（理）如图，已知矩形ABCD中，AB=3，BC=a，若PA⊥平面ABCD，在BC边上取点E，使得PE⊥DE，则满足条件的E点有两个时，求实数a的取值范围．