Question

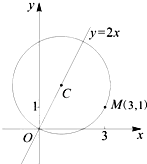
在平面直角坐标系xOy中，已知圆C经过点A（2，0）和点B（3，1），且圆心C在直线x-y-3=0上，过点P（0，1）且斜率为k的直线与圆C相交于不同的两点．
（1）求圆C的方程，同时求出k的取值范围；
（2）是否存在常数k，使得向量

OM

+

ON

与

PC

共线？如果存在，求k值；如果不存在，请说明理由．

Answer 1

考点：圆的标准方程,直线与圆的位置关系

专题：直线与圆

分析：本题（1）可以利用弦的垂直平分线过圆心，求圆心坐标，进而得到圆的方程，再利用直线与圆相交，圆心C到直线的距离d小于半径r，得到斜率k的取值范围；（2）将向量共线条件转化为坐标关系，再利用直线与圆的方程联列的方程组，求出k的值，结合（1）的结论，判断出k的存在性．

解答： 解：（1）∵A（2，0）和点B（3，1），
∴线段AB中点M(

5

2

，

1

2

)，斜率kAB=

1-0

3-2

=1，
∴线段AB的中垂线方程为y=-x+3．
∵圆心C在直线x-y-3=0上，
∴

y=-x+3 x-y-3=0

，
∴圆心C坐标为（3，0）．
半径r=|AC|=1，
∴圆C的方程为（x-3）²+y²=1．
∵直线y=kx+1与圆相交，
∴圆心C到直线的距离d小于半径r．
∴

|3k+1|

1+k2

＜1，
∴-

3

4

＜k＜0．
∴圆心C坐标为（3，0），-

3

4

＜k＜0．
（2）设M（x₁，y₁），N（x₂，y₂），
由

(x-3)2+y2=1 y=kx+1

，
得：（k²+1）x²+（2k-6）x+9=0，
∴x1+x2=

6-2k

k2+1

．
∵

OM

+

ON

=(x1+x2，y1+y2)，

PC

=(3，-1)，
∵

OM

+

ON

与

PC

共线，
∴存在实数λ，使（x₁+x₂，y₁+y₂）=λ（3，-1），
∴3（y₁+y₂）+（x₁+x₂）=0．
∴（3k+1）（x₁+x₂）+6=0，
k=-

3

4

．
由（1）可知k∈(-

3

4

，0)，
故没有符合题意的常数k，
直线不存在．

点评：本题考查了函数方程思想，直线与相交转化为坐标关系，向量共线转化为坐标关系，联列方程组求出k的值．本题有一定的难度，属于中档题．