题目内容
 已知f(x)是定义域为R的奇函数,当x≥0时,f(x)=x2-2x.
已知f(x)是定义域为R的奇函数,当x≥0时,f(x)=x2-2x.(1)求函数f(x)的解析式,并在给出的直角坐标系中画出y=f(x)的图象;
(2)若函数f(x)在区间[m,2m2-m]上单调递减,求实数m的取值范围.
考点:函数奇偶性的性质,函数的图象
专题:作图题,函数的性质及应用
分析:根据奇函数的定义,先设x<0,则-x>0,x≥0时,f(x)=x2-2x.
求出x<0的解析式,最后求函数f(x)的解析式,画图象即可.
(2)据图象可判断条件列出不等式组即可解决.
求出x<0的解析式,最后求函数f(x)的解析式,画图象即可.
(2)据图象可判断条件列出不等式组即可解决.
解答:
解:(1)当x<0时,-x>0f(-x)=x2+2x,f(x)是奇函数,f(-x)=-f(x)得:f(x)=-x2-2x
所以f(x)=
,
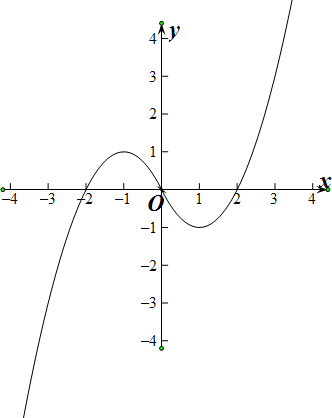
(2)由(1)知f(x)在[-1,1]上为减函数.
∴
解得:-
≤m<0
所以实数m的取值范围为::[-
,0)
所以f(x)=
|
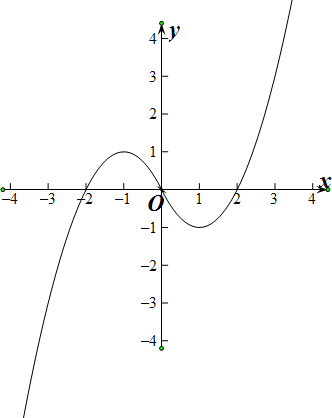
(2)由(1)知f(x)在[-1,1]上为减函数.
∴
|
解得:-
| 1 |
| 2 |
所以实数m的取值范围为::[-
| 1 |
| 2 |
点评:本题考查了奇函数的定义,求解对称区间上的解析式,结合图象求单调区间,及参变量的范围,主要是列不等式,解不等式.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
在△ABC中,角A、B、C的对边分别为a、b、c,则acosB+bcosA等于( )
A、
| ||
| B、b | ||
| C、c | ||
| D、a |
 已知函数f(x)=
已知函数f(x)=