题目内容
已知函数f(x)=
sin2x-cos2x-
,
(1)求函数f(x)在[0,
]的最大值和最小值,并给出取得最值时的x值;
(2)设△ABC的内角A、B、C的对边分别为a,b,c,且c=
,f(C)=0,若sinB=2sinA,求a,b的值.
| ||
| 2 |
| 1 |
| 2 |
(1)求函数f(x)在[0,
| π |
| 2 |
(2)设△ABC的内角A、B、C的对边分别为a,b,c,且c=
| 3 |
考点:三角函数中的恒等变换应用,正弦定理
专题:三角函数的求值,三角函数的图像与性质,解三角形
分析:(1)首先对函数关系式进行恒等变换,把函数的关系式变形成正弦型函数,进一步利用函数的定义域求出函数的值域.
(2)根据(1)的函数关系式,进一步利用正弦和余弦定理求出三角形的边长.
(2)根据(1)的函数关系式,进一步利用正弦和余弦定理求出三角形的边长.
解答:
解:(1)f(x)=
sin2x-cos2x-
=
sin2x-
-
=sin(2x-
)-1
由于:x∈[0,
]
所以:-
≤2x-
≤
则:-
≤sin(2x-
)≤1
则:-
≤f(x)≤0
即当x=
时,函数取最大值,
当x=0时,函数取最小值.
(2)由于f(x)=sin(2x-
)-1
则:f(C)=0
解得:sin(2C-
)-1=0
0<C<π
所以:C=
又:sinB=2sinA
则:b=2a
利用余弦定理得:c2=a2+b2-2abcosC
由于c=
所以解得:a=1
进一步求得:b=2
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| cos2x+1 |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
由于:x∈[0,
| π |
| 2 |
所以:-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
则:-
| 1 |
| 2 |
| π |
| 6 |
则:-
| 3 |
| 2 |
即当x=
| π |
| 3 |
当x=0时,函数取最小值.
(2)由于f(x)=sin(2x-
| π |
| 6 |
则:f(C)=0
解得:sin(2C-
| π |
| 6 |
0<C<π
所以:C=
| π |
| 3 |
又:sinB=2sinA
则:b=2a
利用余弦定理得:c2=a2+b2-2abcosC
由于c=
| 3 |
所以解得:a=1
进一步求得:b=2
点评:本题考查的知识要点:三角函数关系式的恒等变换,利用三角函数的定义域求出函数的值域,余弦和正弦定理的应用,属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若双曲线
-
=1(a>0,b>0)的下焦点是F,点A,B分别是双曲线的两个虚轴端点,且向量
与
的夹角θ的余弦值cosθ=
,则该双曲线一条渐近线的倾斜角为( )
| y2 |
| a2 |
| x2 |
| b2 |
| FA |
| FB |
| 1 |
| 3 |
| A、30° | B、60° |
| C、90° | D、135° |
已知a∈R,b∈R+,e为自然数的底数,则[
ea-ln(2b)]2+(a-b)2的最小值为( )
| 1 |
| 2 |
| A、(1-ln2)2 | ||
| B、2(1-ln2)2 | ||
| C、1+ln2 | ||
D、
|
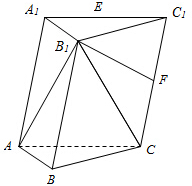 已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.
已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.