题目内容
7．有一项活动，需在3名老师，8名男同学和5名女同学中选人参加．（1）若只需一人参加，有多少种不同方法？
（2）若需老师、男同学、女同学各一人参加，有多少种不同选法？
（3）若需一名老师，一名学生参加，有多少种不同选法？
分析 根据分类和分步计数原理可得．
解答 解：（1）根据分类计数原理，可得只需一人参加，有3+8+5=16种不同方法，
（2）根据分步计数原理可得，需老师、男同学、女同学各一人参加，有3×8×5=120种，
（3）根据分类和分步计数原理可得，需一名老师，一名学生参加，有3×（8+5）=39种．
点评 本题考查排列、组合及简单计数问题，解题的关键是正确理解题设中的事件，及理解计数原理，本题考查了分类的及运算的能力．
练习册系列答案
相关题目
17．设p：?x∈R，x2-4x+3m＞0，q：f（x）=x3+2x2+mx+1在（-∞，+∞）内单调递增，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
18．平面向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{2π}{3}$，$\overrightarrow a=（{3，0}），|{\overrightarrow b}|=2$，则$|{\overrightarrow a+2\overrightarrow b}|$等于（ ）
| A． | 13 | B． | $\sqrt{37}$ | C． | $\sqrt{13}$ | D． | 3 |
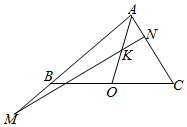如图所示，在△ABC中，AO是BC边上的中线，K为AO上一点，且$\overrightarrow{AO}$=2$\overrightarrow{AK}$，过点K的直线分别交直线AB、AC于不同的两点M，N，若$\overrightarrow{AB}$=m$\overrightarrow{AM}$，$\overrightarrow{AC}$=n$\overrightarrow{AN}$，则m+n=4．
19．已知点P（x，y）在不等式组$\left\{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$表示的平面区域上运动，则z=x2+y2的取值范围是（ ）
| A． | [$\frac{3}{5}$，4] | B． | [$\frac{4}{5}$，5] | C． | [$\frac{4}{5}$，6] | D． | [$\frac{3}{5}$，5] |