题目内容
17．设p：?x∈R，x2-4x+3m＞0，q：f（x）=x3+2x2+mx+1在（-∞，+∞）内单调递增，则p是q的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 函数单调递增等价于导函数大于等于0恒成立，故判别式小于等于0，求出命题p的等价条件，得到p，q的关系．从而得解．
解答 解：∵p：?x∈R，x2-4x+3m＞0，
∴△=16-12m＜0，解得：m＞$\frac{4}{3}$，
q：f（x）=x3+2x2+mx+1在（-∞，+∞）内单调递增，
∴f′（x）=3x2+4x+m≥0恒成立，
∴△=16-12m≤0，
解得m≥$\frac{4}{3}$，
∴p是q的充分不必要条件，
故选：A．
点评 本题考查利用导数求函数的单调性及必要条件、充分条件、充要条件的判断．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
7．
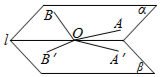如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）
如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）| A． | ∠A′OB′为钝角 | B． | ∠A′OB′＞∠AOB | ||
| C． | ∠AOB+∠AOA′＜π | D． | ∠B′OB+∠BOA+∠AOA′＞π |
8．为普及学生安全逃生知识与安全防护能力，某学校高一年级举办了安全知识与安全逃生能力竞赛，该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛，现将所有参赛选手参加笔试的成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
（1）求出上表中的x，y，z，s，p的值；
（2）按规定，预赛成绩不低于90分的选手参加决赛．已知高一（2）班有甲、乙两名同学取得决赛资格，记高一（2）班在决赛中进入前三名的人数为X，求X的分布列和数学期望．
| 分数（分数段） | 频数（人数） | 频率 |
| [60，70） | 9 | x |
| [70，80） | y | 0.38 |
| [80，90） | 16 | 0.32 |
| [90，100） | z | s |
| 合计 | p | 1 |
（2）按规定，预赛成绩不低于90分的选手参加决赛．已知高一（2）班有甲、乙两名同学取得决赛资格，记高一（2）班在决赛中进入前三名的人数为X，求X的分布列和数学期望．
6．已知点P是函数y=sin（2x+α）图象与x轴的一个交点，A，B为P点右侧距离点P最近的一个最高点和最低点，则$\overrightarrow{PA}$•$\overrightarrow{PB}$=（ ）
| A． | $\frac{{π}^{2}}{4}$-1 | B． | $\frac{3{π}^{2}}{16}$-1 | C． | $\frac{3{π}^{2}}{4}$-1 | D． | $\frac{{π}^{2}}{8}$-1 |