题目内容
16．已知角θ的始边与x轴的非负半轴重合，终边过点M（-3，4），则cos2θ的值为（ ）| A． | $-\frac{7}{25}$ | B． | $\frac{7}{25}$ | C． | $-\frac{24}{25}$ | D． | $\frac{24}{25}$ |
分析 由条件利用任意角的三角函数的定义，求出sinθ，利用二倍角公式即可计算得解．
解答 解：∵角θ的终边经过点P（-3，4），
∴x=-3，y=4，r=|OP|=5，
∴sinθ=$\frac{y}{r}$=$\frac{4}{5}$，则cos2θ=1-2sin2θ=-$\frac{7}{25}$．
故选：A．
点评 本题主要考查任意角的三角函数的定义，两点间的距离公式，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
7．执行如图所救援程序框图，输出s的值为（ ）
| A． | 1 | B． | $\sqrt{2015}$-1 | C． | $\sqrt{2016}$-1 | D． | $\sqrt{2017}$-1 |
8．已知集合A={-1，0，1，3，4，5}，B={x|x2-4x+3≤0}，则A∩B=（ ）
| A． | {1} | B． | {3} | C． | {1，3} | D． | ∅ |
5．
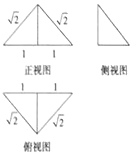一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）
一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）| A． | $\frac{4π}{3}$ | B． | 4π | C． | $\frac{2π}{3}$ | D． | 2π |
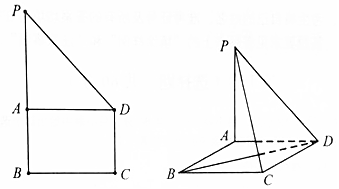如图，在直角梯形PBCD中，PB∥DC，DC⊥BC，点A在边PB上，AD∥BC，PB=3BC=6，现沿AD将△PAD折起，使平面PAD⊥平面ABCD．