题目内容
15.已知圆O:x2+y2=1与直线l:ax+by+2=0相切,则动点P(2a,3b)在直角坐标平面xoy内的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{36}=1$.分析 利用已知条件列出方程化简求解即可.
解答 解:圆O:x2+y2=1与直线l:ax+by+2=0相切,
可得:$\frac{|2|}{\sqrt{{a}^{2}+{b}^{2}}}=1$,即a2+b2=4,
动点P(2a,3b)设为(x,y),则a=$\frac{x}{2}$,b=$\frac{y}{3}$,代入a2+b2=4,
可得:$\frac{x^2}{16}+\frac{y^2}{36}=1$.
故答案为:$\frac{x^2}{16}+\frac{y^2}{36}=1$.
点评 本题考查轨迹方程的求法,考查计算能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
5.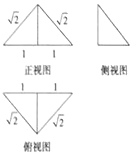 一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )
一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )
 一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )
一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )| A. | $\frac{4π}{3}$ | B. | 4π | C. | $\frac{2π}{3}$ | D. | 2π |
3.已知命题p:?x∈R,x2-2x-1≥0,则¬p是( )
| A. | ?x∈R,x2-2x-1≥0 | B. | ?x∈R,x2-2x-1<0 | C. | ?x∈R,x2-2x-1<0 | D. | ?x∈R,x2-2x-1≤0 |
10.已知函数f(x)=x•cosx,则$f'({\frac{π}{2}})$的值为( )
| A. | $-\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | 1 | D. | -1 |
7.如图,正六边形ABCDEF中,$\overrightarrow{BC}$$+\overrightarrow{DE}$$+\overrightarrow{AF}$等于( )
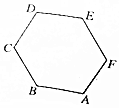

| A. | $\overrightarrow{EB}$ | B. | $\overrightarrow{BE}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CF}$ |
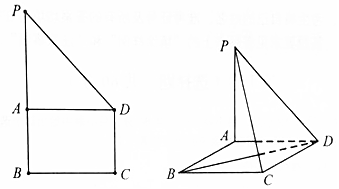 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.