题目内容
14．若$tan（{\frac{π}{2}-α}）=2$，则$\frac{sinα-cosα}{2sinα+cosα}$=-$\frac{1}{4}$．分析 根据同角三角函数关系式和诱导公式即可求值
解答 解：由$tan（{\frac{π}{2}-α}）=2$，可得：$\frac{cosα}{sinα}=2$，
得cosα=2sinα．
则$\frac{sinα-cosα}{2sinα+cosα}$=$\frac{sinα-2sinα}{2sin+2sinα}=-\frac{1}{4}$，
故答案为：$-\frac{1}{4}$
点评 本题主要考察了同角三角函数关系式和诱导公式的计算．属于基本知识的考查．
练习册系列答案
相关题目
5．
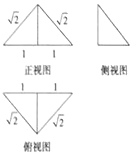一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）
一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）| A． | $\frac{4π}{3}$ | B． | 4π | C． | $\frac{2π}{3}$ | D． | 2π |
2．已知全集U=R，集合A={x|x＜-$\frac{1}{2}$或x＞1}，B={x|-1≤x≤2，x∈Z}，则图中阴影部分所表示的集合等于（ ）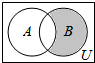
| A． | {-1，2} | B． | {-1，0} | C． | {0，1} | D． | {1，2} |
9．已知点A（-1，2），B（2，3），直线l：kx-y-k+1=0与线段AB相交，则实数k的取值范围是（ ）
| A． | -$\frac{1}{2}$≤k≤2 | B． | k≤-$\frac{1}{2}$或k≥2 | C． | -2≤k≤$\frac{1}{2}$ | D． | k≤-2或k≥$\frac{1}{2}$ |
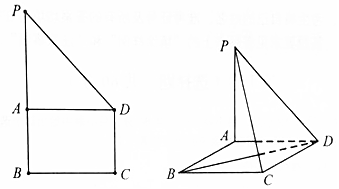如图，在直角梯形PBCD中，PB∥DC，DC⊥BC，点A在边PB上，AD∥BC，PB=3BC=6，现沿AD将△PAD折起，使平面PAD⊥平面ABCD．
3．已知命题p：?x∈R，x2-2x-1≥0，则￢p是（ ）
| A． | ?x∈R，x2-2x-1≥0 | B． | ?x∈R，x2-2x-1＜0 | C． | ?x∈R，x2-2x-1＜0 | D． | ?x∈R，x2-2x-1≤0 |