题目内容
在三棱锥P-ABC中,∠ABC=90°,PB丄平面ABC,AB=BC=2
,PB=2,则点B到平面PAC的距离是 .
| 2 |
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:利用等体积法,计算点B到平面PAC的距离.
解答:
 解:由题意,△PAC中,PC=PA=2
解:由题意,△PAC中,PC=PA=2
,AC=4,
∴S△PAC=
×4×2
=4
,
设点B到平面PAC的距离是h,则
×
×2
×2
×2=
×4
h,
∴h=
.
故答案为:
.
 解:由题意,△PAC中,PC=PA=2
解:由题意,△PAC中,PC=PA=2| 3 |
∴S△PAC=
| 1 |
| 2 |
| 2 |
| 2 |
设点B到平面PAC的距离是h,则
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
∴h=
| 2 |
故答案为:
| 2 |
点评:本题考查点B到平面PAC的距离,考查等体积法,比较基础.

练习册系列答案
相关题目
已知f:x→x2是集合A到集合B={0,1,4}的一个映射,则集合A中的元素个数最多有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
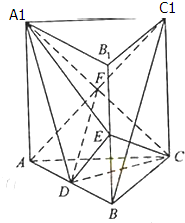 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4