题目内容
将面积为S的平面凸四边形的第i条边的边长记为ai(i=1,2,3,4),此四边形内任一点P到第i条边的距离记为hi(i=1,2,3,4),若
=
=
=
=k,则
ihi=
;类比以上性质,将体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若
=
=
=
=k,则 .
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
| 4 |
 |
| i=1 |
| 2S |
| k |
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S4 |
| 4 |
考点:类比推理
专题:规律型,推理和证明
分析:由
=
=
=
=k可得ai=ik,P是该四边形内任意一点,将P与四边形的四个定点连接,得四个小三角形,四个小三角形面积之和为四边形面积,即采用分割法求面积;同理对三棱值得体积可分割为5个已知底面积和高的小棱锥求体积.
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
解答:
解:根据三棱锥的体积公式V=
Sh.
得:
S1H1+
S2H2+
S3H3+
S4H4=V,
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+H2+3H3+4H4=
故答案为:H1+H2+3H3+4H4=
.
| 1 |
| 3 |
得:
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+H2+3H3+4H4=
| 3V |
| k |
故答案为:H1+H2+3H3+4H4=
| 3V |
| k |
点评:本题主要考查三棱锥的体积计算和运用类比思想进行推理的能力.解题的关键是理解类比推理的意义,掌握类比推理的方法.

练习册系列答案
相关题目
公差不为0的等差数列{an}的第2,3,7项恰为等比数列{bn}的连续三项,则{bn}的公比为( )
| A、1 | B、2 | C、3 | D、4 |
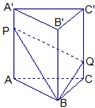 如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为
如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为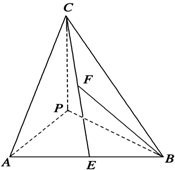 如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.
如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.