题目内容
设8（a3-1）=（a-1）（a+1）（a2+a+1），且a≠1，则a的值是（ ）
| A、7 | B、15 | C、35 | D、63 |
考点：有理数指数幂的化简求值
专题：计算题
分析：由已知中8（a3-1）=（a-1）（a+1）（a2+a+1），且a≠1，结合立方差公式，可得a+1=8，进而得到答案．
解答：
解：∵8（a3-1）=（a-1）（a+1）（a2+a+1）=（a+1）（a3-1），且a≠1，
故a+1=8，
解得：a=7，
故选：A
故a+1=8，
解得：a=7，
故选：A
点评：本题考查的知识点是立方差公式，其中根据立方差公式，对已知等式进行变形，得到a+1=8，是解答的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
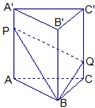如图直三棱柱ABC-A1B1C1的体积为120，点P、Q分别在侧棱AA1和CC1上，AP=C1Q，则四棱锥B-APQC的体积为
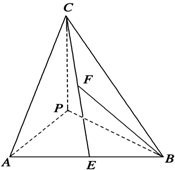如图，四面体P-ABC中，PA、PB、PC两两垂直，PA=PB=2，PC=4，E是AB的中点，F是CE的中点．