题目内容
已知平面向量
=（2，-1），
=（x，1），若
⊥
，则x= ．
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由向量的垂直可得数量积为0，可得x的方程，解方程可得．
解答：
解：∵
=（2，-1），
=（x，1），且
⊥
，
∴2x+1×（-1）=0，解得x=
．
故答案为：
．
| a |
| b |
| a |
| b |
∴2x+1×（-1）=0，解得x=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查平面向量的垂直关系，即数量积为0，属基础题．
练习册系列答案
相关题目
函数y=f（x）有f（x）=-f（x+1），且x∈[-1，1]时f（x）=1-x2．函数g（x）=
则函数h（x）=f（x）-g（x）在区间[-5，4]内的零点个数为（ ）
|
| A、7 | B、8 | C、9 | D、10 |
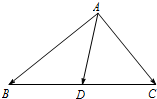如图，点D是线段BC的中点，BC=6，且|| AB |
| AC |
| AB |
| AC |
| AD |
| A、6 | ||
B、2
| ||
| C、3 | ||
D、
|
已知函数f（x）=
若三个正实数x1，x2，x3互不相等，且满足f（x1）=f（x2）=f（x3），则x1x2x3的取值范围是（ ）
|
| A、（20，24） |
| B、（10，12） |
| C、（5，6） |
| D、（1，10） |