题目内容
将圆心角为120°,面积为3π的扇形,作为圆锥的侧面,圆锥的表面积为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:运圆的面积公式求出R,母线长,在求出圆锥的底面半径,即可利用公式求解.
解答:
解:∵圆心角为120°,面积为3π的扇形,
∴
πR2=3π,R=3,
∴圆锥母线长为:l=3,
∵πrl=3π,
∴r=1,
∴S底=πr2=π,
∴圆锥的表面积为3π+π=4π,
故答案为:4π.
∴
| 2 |
| 3 |
∴圆锥母线长为:l=3,
∵πrl=3π,
∴r=1,
∴S底=πr2=π,
∴圆锥的表面积为3π+π=4π,
故答案为:4π.
点评:本题考查了圆锥的性质,面积公式,属于计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,b∈R,且a>b,则( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
D、(
|
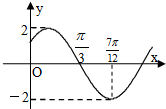 如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )A、y=2sin(2x-
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x-
| ||||
D、y=2sin(2x+
|
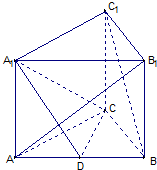 如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.
如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.