题目内容
已知函数f(x)=2sin(πx+
)
(1)当x∈[-
,
]时,求f(x)的最值;
(2)若f(
)=
,求cos(
-α)的值.
| π |
| 6 |
(1)当x∈[-
| 1 |
| 2 |
| 1 |
| 2 |
(2)若f(
| α |
| 2π |
| 1 |
| 4 |
| 2π |
| 3 |
考点:正弦函数的图象
专题:三角函数的求值
分析:(1)直接利用三角函数的单调性和定义域求解.
(2)首先利用三角函数角的恒等变换,求出sin(
+
)=
进一步求出cos(
-
)=cos[
-(
+
)]=sin(
+
)=
最后求出结果.
(2)首先利用三角函数角的恒等变换,求出sin(
| α |
| 2 |
| π |
| 6 |
| 1 |
| 8 |
| π |
| 3 |
| α |
| 2 |
| π |
| 2 |
| π |
| 6 |
| α |
| 2 |
| π |
| 6 |
| α |
| 2 |
| 1 |
| 8 |
解答:
解:(1)函数f(x)=2sin(πx+
)
当x∈[-
,
]时,利用函数的单调性,
f(x)max=2,f(x)min=-
(2)由f(
)=
,所以有:2sin(π•
+
)=2sin(
+
)=
所以sin(
+
)=
而cos(
-
)=cos[
-(
+
)]=sin(
+
)=
所以cos(
-α)=cos[2(
-
)]=2cos2(
-
)-1
即cos(
-α)=2sin2(
+
)-1=-
| π |
| 6 |
当x∈[-
| 1 |
| 2 |
| 1 |
| 2 |
f(x)max=2,f(x)min=-
| 3 |
(2)由f(
| α |
| 2π |
| 1 |
| 4 |
| α |
| 2π |
| π |
| 6 |
| α |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
所以sin(
| α |
| 2 |
| π |
| 6 |
| 1 |
| 8 |
而cos(
| π |
| 3 |
| α |
| 2 |
| π |
| 2 |
| π |
| 6 |
| α |
| 2 |
| π |
| 6 |
| α |
| 2 |
| 1 |
| 8 |
所以cos(
| 2π |
| 3 |
| π |
| 3 |
| α |
| 2 |
| π |
| 3 |
| α |
| 2 |
即cos(
| 2π |
| 3 |
| α |
| 2 |
| π |
| 6 |
| 31 |
| 32 |
点评:本题考查的知识要点:利用三角函数的定义域求值域,角的恒等变换及相关的运算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
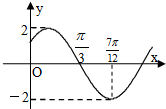 如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )A、y=2sin(2x-
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x-
| ||||
D、y=2sin(2x+
|
已知命题p:?x∈R,2x>0;命题q:在曲线y=cosx上存在斜率为
的切线,则下列判断正确的是( )
| 2 |
| A、p是假命题 |
| B、q是真命题 |
| C、p∧(¬q)是真命题 |
| D、(¬p)∧q是真命题 |
在△ABC中,a,b,c分别为角A、B、C的对边,若边a,b,c成等差数列,则∠B的范围是( )
A、0<B≤
| ||
B、0<B≤
| ||
C、0<B≤
| ||
D、
|
在数列{xn}中,
=
+
(n≥2),且x2=
,x4=
,则x10等于( )
| 2 |
| xn |
| 1 |
| xn-1 |
| 1 |
| xn+1 |
| 2 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|