题目内容
14.已知抛物线y2=2px(p>0)上的一点M(1,t)(t>0)到焦点的距离为5,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值为2.分析 设M点到抛物线准线的距离为d,由已知可得p值,由双曲线的一条渐近线与直线AM平行,则$\frac{4}{1+a}$=$\frac{3}{a}$,解得实数a的值.
解答 解:设M点到抛物线准线的距离为d,
则丨MF丨=d=1+$\frac{p}{2}$=5,则p=8,
所以抛物线方程为y2=16x,M的坐标为(1,4);
又双曲线的左顶点为A(-a,0),渐近线为y=±$\frac{3}{a}$,
直线AM的斜率k=$\frac{4-0}{1+a}$=$\frac{4}{1+a}$,由$\frac{4}{1+a}$=$\frac{3}{a}$,解得a=3.
∴a的值为3,
故答案为:3.
点评 本题考查的知识点是抛物线的简单性质,双曲线的简单性质,是抛物线与双曲线的综合应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知曲线C:y=sin(2x+φ)(|φ|<$\frac{π}{2}$)的一条对称轴方程为x=$\frac{π}{6}$,曲线C向左平移θ(θ>0)个单位长度,得到的曲线E的一个对称中心为($\frac{π}{6}$,0),则|φ-θ|的最小值是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
2.已知集合A={x|x2+x-6>0},集合B={x|-1<x<3},若a∈(A∪B),则a可以是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
9.已知A(1,-2),B(4,2),则与$\overrightarrow{AB}$反方向的单位向量为( )
| A. | (-$\frac{3}{5}$,$\frac{4}{5}$) | B. | ($\frac{3}{5}$,-$\frac{4}{5}$) | C. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | D. | ($\frac{3}{5}$,$\frac{4}{5}$) |
19.已知e为自然对数的底,a=($\frac{2}{e}$)-0.2,b=($\frac{e}{2}$)0.4,c=$lo{g}_{\frac{2}{e}}e$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | a<b<c |
6.设复数z满足(1+i)z=-2i,i为虚数单位,则z=( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
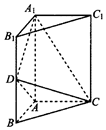 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点. 如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°,点E是线段PA上靠近点A的三等分点.
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°,点E是线段PA上靠近点A的三等分点.