题目内容
2.已知集合A={x|x2+x-6>0},集合B={x|-1<x<3},若a∈(A∪B),则a可以是( )| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
分析 先分别求出集合A和集合B,从而求出A∪B,再由a∈(A∪B),能求出a.
解答 解:∵集合A={x|x2+x-6>0}={x|x<-3或x>2},
集合B={x|-1<x<3},
∴A∪B={x<-3或x>-1},
∴a∈(A∪B),∴a可以是3.
故选:D.
点评 本题考查并集的求法及应用,是基础题,解题时要认真审题,注意并集定义的合理运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
10.已知函数f(x)=$\frac{ln(2x)}{x}$,关于x的不等式f2(x)+af(x)>0只有两个整数解,则实数a的取值范围是( )
| A. | $(-ln2,-\frac{1}{3}ln6]$ | B. | $(-\frac{1}{e},-\frac{ln6}{3}]$ | C. | $[\frac{1}{3}ln6,ln2)$ | D. | $[\frac{ln6}{3},\frac{2}{e})$ |
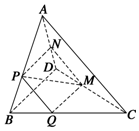 如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).
如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).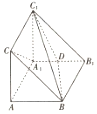 如图,在直三棱柱ABC-A1B1C1中,D是A1B1的中点.
如图,在直三棱柱ABC-A1B1C1中,D是A1B1的中点.