题目内容
5.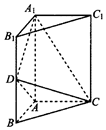 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.(Ⅰ)证明:平面A1DC⊥平面ADC;
(Ⅱ)求平面A1DC与平面ABC所成二面角的余弦值.
分析 (Ⅰ)由侧棱AA1⊥底面ABC,得AA1⊥AC,结合AB⊥AC,利用线面垂直的判定可得AC⊥平面ABB1A1,进一步得到AC⊥A1D,AB=a,通过求解三角形可得AD⊥A1D,得到A1D⊥平面ADC.由线面垂直的判定可得平面A1DC⊥平面ADC;
(Ⅱ)分别以AB,AC,AA1所在直线为x,y,z轴建立空间直角坐标系,设AB=1,求得A,D,C,A1的坐标,进一步求出平面ABC与平面A1DC的一个法向量,由两法向量所成角的余弦值可得平面A1DC与平面ABC所成二面角的余弦值.
解答 (Ⅰ)证明:∵侧棱AA1⊥底面ABC,∴AA1⊥AC,
又∵AB⊥AC,AB∩AC=A,∴AC⊥平面ABB1A1,
∵A1D?平面ABB1A1,∴AC⊥A1D,
设AB=a,由$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
得$AD={A_1}D=\sqrt{2}a$,AA1=2a,
则$A{D^2}+{A_1}{D^2}=2{a^2}$+$2{a}^{2}=4{a}^{2}=A{{A}_{1}}^{2}$,
∴AD⊥A1D,
∵AD∩AC=A, ∴A1D⊥平面ADC.
∴A1D⊥平面ADC.
又∵A1D?平面A1DC,∴平面A1DC⊥平面ADC;
(Ⅱ)解:如图所示,分别以AB,AC,AA1所在直线为x,y,z轴建立空间直角坐标系,
不妨设AB=1,则A(0,0,0),D(1,0,1),C(0,1,0),A1(0,0,2).
显然$\overrightarrow m=({0,0,1})$是平面ABC的一个法向量,
设平面A1DC的法向量$\overrightarrow n=({x,y,z})$,
由$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{{A_1}D}=0\\ \overrightarrow n•\overrightarrow{{A_1}C}=0\end{array}\right.$$⇒\left\{\begin{array}{l}x-z=0\\ y-2z=0\end{array}\right.$
令z=1,得平面A1DC的一个法向量$\overrightarrow n=({1,2,1})$,
∴$cos\left?{\overrightarrow m,\overrightarrow n}\right>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}$=$\frac{1}{{\sqrt{6}}}=\frac{{\sqrt{6}}}{6}$,
即平面A1DC与平面ABC所成二面角的余弦值为$\frac{{\sqrt{6}}}{6}$.
点评 本题考查线面垂直的判定和性质,考查空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.

| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 关于直线y=x对称 |
| A. | 0 | B. | 2 | C. | 4 | D. | 5 |
| A. | $(-ln2,-\frac{1}{3}ln6]$ | B. | $(-\frac{1}{e},-\frac{ln6}{3}]$ | C. | $[\frac{1}{3}ln6,ln2)$ | D. | $[\frac{ln6}{3},\frac{2}{e})$ |
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | C. | 若m⊥n,n?α,则m⊥α | D. | 若m∥n,m∥α,则n∥α |