题目内容
19．已知e为自然对数的底，a=（$\frac{2}{e}$）-0.2，b=（$\frac{e}{2}$）0.4，c=$lo{g}_{\frac{2}{e}}e$，则a，b，c的大小关系是（ ）| A． | c＜a＜b | B． | c＜b＜a | C． | b＜a＜c | D． | a＜b＜c |
分析 由0＜a=（$\frac{2}{e}$）-0.2=$（\frac{e}{2}）^{0.2}$＜b=（$\frac{e}{2}$）0.4，c=$lo{g}_{\frac{2}{e}}e$＜0，即可得出．
解答 解：∵0＜a=（$\frac{2}{e}$）-0.2=$（\frac{e}{2}）^{0.2}$＜b=（$\frac{e}{2}$）0.4，c=$lo{g}_{\frac{2}{e}}e$＜0，
∴b＞a＞c，
故选：A．
点评 本题考查了指数函数对数函数，考查了推理能力与计算能力，属于基础题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
9．已知是某几何体的三视图，则该几何体的体积为（ ）
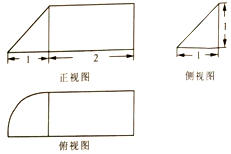
| A． | $\frac{1}{3}+\frac{π}{12}$ | B． | $1+\frac{π}{12}$ | C． | $\frac{1}{3}+\frac{π}{4}$ | D． | $1+\frac{π}{4}$ |
10．已知函数f（x）=$\frac{ln（2x）}{x}$，关于x的不等式f2（x）+af（x）＞0只有两个整数解，则实数a的取值范围是（ ）
| A． | $（-ln2，-\frac{1}{3}ln6]$ | B． | $（-\frac{1}{e}，-\frac{ln6}{3}]$ | C． | $[\frac{1}{3}ln6，ln2）$ | D． | $[\frac{ln6}{3}，\frac{2}{e}）$ |
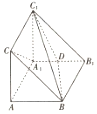如图，在直三棱柱ABC-A1B1C1中，D是A1B1的中点．
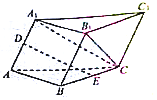如图，在三棱柱ABC-A1B1C1中，侧面ACC1A1⊥底面ABC，∠A1AC=60°，AC=2AA1=4，点D，E分别是AA1，BC的中点．