题目内容
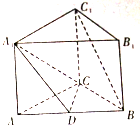如图，直三棱柱ABC-A 11C1中，AC=BC=1，∠ACB=90°，点D为AB的中点．（1）求证：BC1∥面A1DC；
（2）若AA1=
| ||
| 2 |
考点：与二面角有关的立体几何综合题,直线与平面平行的判定
专题：空间位置关系与距离,空间角
分析：（1）连接AC1，与AC1交于点E，连接ED，由已知得DE∥BC1，由此能证明BC1∥面A1DC．
（2）由已知得∠A1DA为二面角A1-CD-A的平面角，由此能求出二面角A1-CD-B的平面角的大小．
（2）由已知得∠A1DA为二面角A1-CD-A的平面角，由此能求出二面角A1-CD-B的平面角的大小．
解答：
（1）证明：连接AC1，与AC1交于点E，连接ED，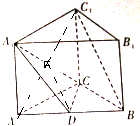
则E为AC1的中点，又点D是AB中点，
则DE∥BC1，
而DE?平面A1DC，
BC1不包含于面A1DC，
∴BC1∥面A1DC．
（2）解：∵二面角A1-CD-B的平面角与二面角A1-CD-A的平面角互补，
又∵CD⊥AB，CD⊥AA1，
∴CD⊥面ADA1，∴CD⊥A1D，
∴∠A1DA为二面角A1-CD-A的平面角，
在Rt△A1AD中，∵AA1=
=AD，
∴∠A1DA=45°，
∴二面角A1-CD-A的平面角的大小为45°，
∴二面角A1-CD-B的平面角的大小为135°．
则E为AC1的中点，又点D是AB中点，
则DE∥BC1，
而DE?平面A1DC，
BC1不包含于面A1DC，
∴BC1∥面A1DC．
（2）解：∵二面角A1-CD-B的平面角与二面角A1-CD-A的平面角互补，
又∵CD⊥AB，CD⊥AA1，
∴CD⊥面ADA1，∴CD⊥A1D，
∴∠A1DA为二面角A1-CD-A的平面角，
在Rt△A1AD中，∵AA1=
| ||
| 2 |
∴∠A1DA=45°，
∴二面角A1-CD-A的平面角的大小为45°，
∴二面角A1-CD-B的平面角的大小为135°．
点评：本题考查直线与平面平行的证明，考查二面角的平面角的大小的求法，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
把-495°表示成K•360°+θ（k∈Z）的形式，其中使|θ|最小的θ值是（ ）
| A、-135° | B、-45° |
| C、45° | D、135° |
已知正项等比数列{an}满足a3•a2n-3=4n（n＞1），则log2a1+log2a3+log2a5+…+log2a2n-1=（ ）
| A、n2 |
| B、（n+1）2 |
| C、n（2n-1） |
| D、（n-1）2 |
已知集合A={x|-1≤x≤3}，集合B={x|
＜0}，则A∪B=（ ）
| 1 |
| x |
| A、{x|-1＜x＜0} |
| B、{x|-1≤x＜0} |
| C、{x|x＜0} |
| D、{x|x≤3} |
三个数e-
，log0.23，lnπ的大小关系为（ ）
| 2 |
A、log0.23＜e-
| ||
B、log0.23＜lnπ＜e-
| ||
C、e-
| ||
D、log0.23＜lnπ＜e-
|
如图，已知抛物线C：y2=x和⊙M：（x-4）2+y2=1，过抛物线C上一点H（x0，y0）（y0≥1）做两条直线与⊙M相切于A、B两点，分别交抛物线于E、F两点．