题目内容
求证:sin(α+β)cosα-
[sin(2α+β)-sinβ]=sinβ
| 1 |
| 2 |
考点:三角函数中的恒等变换应用
专题:证明题,三角函数的求值
分析:先利用两角和求得sin(2α+β)即sin(α+α+β)的表达式代入原式,整理可证明.
解答:
解:∵sin(2α+β)=sin(α+α+β)=sinαcos(α+β)+cosαsin(α+β),
∴sin(α+β)cosα-
[sin(2α+β)-sinβ]
=sin(α+β)cosα-
sinαcos(α+β)-
cosαsin(α+β)+
sinβ
=
cosαsin(α+β)-
sinαcos(α+β)+
sinβ
=
sin(α+β-α)+
sinβ
=
sinβ+
sinβ
=sinβ.
故原式成立.
∴sin(α+β)cosα-
| 1 |
| 2 |
=sin(α+β)cosα-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=sinβ.
故原式成立.
点评:本题主要考查了三角形恒等变换的应用.在解题的时候,有时需要有意识的凑出角的形式,来解决.如本题就是把2α+β转化成α+(α+β).

练习册系列答案
相关题目
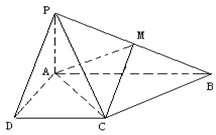 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= 气象台预报,距离S岛正东方向300km的A处有一台风形成,并以每小时30km的速度向北偏西30°的方向移动,在距台风中心处不超过270km以内的地区将受到台风的影响.问:
气象台预报,距离S岛正东方向300km的A处有一台风形成,并以每小时30km的速度向北偏西30°的方向移动,在距台风中心处不超过270km以内的地区将受到台风的影响.问: