题目内容
已知函数f(x)=sin2x+2
sinxcosx+3cos2x.
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)已知f(a)=3,且α∈(0,
),求α的值.
| 3 |
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)已知f(a)=3,且α∈(0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)利用二倍角公式和两角和公式对函数解析式进行化简整理求得函数解析式,利用三角函数的性质求得其最小正周期T和单调增区间.
(Ⅱ)利用f(a)=3求得sin(2a+
)的值,进而求得a.
(Ⅱ)利用f(a)=3求得sin(2a+
| π |
| 6 |
解答:
解:(Ⅰ)∵f(x)=sin2x+2
sinxcosx+3cos2x,
=
sin2x+2-
+1
=
sin2x+cos2x+2
=2sin(2x+
)+2.
所以最小正周期为:T=
=π
当-
+2kπ≤2x+
≤
+2kπ(k∈Z),即-
+kπ≤x≤
+kπ(k∈Z)时函数单调增,
∴函数f(x)的单调增区间为[-
+kπ,
+kπ](k∈Z).
(Ⅱ)∵f(x)=2sin(2x+
)+2,
∴f(α)=2sin(2α+
)+2=3,
∴sin(2α+
)=
,
∵α∈(0,
),
∴2α+
∈(
,
),
∴2α+
=
,
∴α=
.
| 3 |
=
| 3 |
| 1-cos2x |
| 2 |
=
| 3 |
=2sin(2x+
| π |
| 6 |
所以最小正周期为:T=
| 2π |
| 2 |
当-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数f(x)的单调增区间为[-
| π |
| 3 |
| π |
| 6 |
(Ⅱ)∵f(x)=2sin(2x+
| π |
| 6 |
∴f(α)=2sin(2α+
| π |
| 6 |
∴sin(2α+
| π |
| 6 |
| 1 |
| 2 |
∵α∈(0,
| π |
| 2 |
∴2α+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴2α+
| π |
| 6 |
| 5π |
| 6 |
∴α=
| π |
| 3 |
点评:本题主要考查了三角函数的恒等变换的应用,三角函数的图象和性质.要充分利用好三角函数的图象,利用数形结合的思想来解决三角函数的相关问题.

练习册系列答案
相关题目
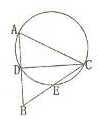 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.