题目内容
阅读:已知a、b∈(0,+∞),a+b=1,求y=
+
的最小值.解法如下:y=
+
=(
+
)(a+b)=
+
+3≥3+2
,当且仅当
=
,即a=
-1,b=2-
时取到等号,则y=
+
的最小值为3+2
.应用上述解法,求解下列问题:
(1)已知a,b,c∈(0,+∞),a+b+c=1,求y=
+
+
的最小值;
(2)已知x∈(0,
),求函数y=
+
的最小值;
(3)已知正数a1、a2、a3,…,an,a1+a2+a3+…+an=1,求证:S=
+
+
+…+
≥
.
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
| 2 |
| b |
| a |
| 2a |
| b |
| 2 |
| 2 |
| 1 |
| a |
| 2 |
| b |
| 2 |
(1)已知a,b,c∈(0,+∞),a+b+c=1,求y=
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(2)已知x∈(0,
| 1 |
| 2 |
| 1 |
| x |
| 8 |
| 1-2x |
(3)已知正数a1、a2、a3,…,an,a1+a2+a3+…+an=1,求证:S=
| a12 |
| a1+a2 |
| a22 |
| a2+a3 |
| a32 |
| a3+a4 |
| an2 |
| an+a1 |
| 1 |
| 2 |
考点:基本不等式
专题:不等式的解法及应用
分析:利用“乘1法”和基本不等式即可得出.
解答:
解(1)∵a+b+c=1,
∴y=
+
+
=(a+b+c)(
+
+
)=3+(
+
+
+
+
+
)≥3+2
+2
+2
=9,
当且仅当a=b=c=
时取等号.即y=
+
+
的最小值为9.
(2)y=
+
=(
+
)(2x+1-2x)=10+2•
+8•
,
而x∈(0,
),∴2•
+8•
≥2
=8,
当且仅当
=
,即x=
∈(0,
)时取到等号,则y≥18,
∴函数y=
+
的最小值为18.
(3)∵a1+a2+a3+…+an=1,
∴2S=(
+
+
+…+
)[(a1+a2)+(a2+a3)+…+(an+a1)]
=(
+
+…+
)+[
(a2+a3)+
(a1+a2)+…+
(a1+a2)+
(a3+a4)+…]
≥(
+
+…+
)+(2a1a2+2a2a3+…+2ana1)=(a1+a2+…+an)2=1.
当且仅当a1=a2=…=an=
时取到等号,则S≥
.
∴y=
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
|
|
|
当且仅当a=b=c=
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(2)y=
| 2 |
| 2x |
| 8 |
| 1-2x |
| 2 |
| 2x |
| 8 |
| 1-2x |
| 1-2x |
| 2x |
| 2x |
| 1-2x |
而x∈(0,
| 1 |
| 2 |
| 1-2x |
| 2x |
| 2x |
| 1-2x |
|
当且仅当
| 2(1-2x) |
| 2x |
| 8•2x |
| 1-2x |
| 1 |
| 6 |
| 1 |
| 2 |
∴函数y=
| 1 |
| x |
| 8 |
| 1-2x |
(3)∵a1+a2+a3+…+an=1,
∴2S=(
| a12 |
| a1+a2 |
| a22 |
| a2+a3 |
| a32 |
| a3+a4 |
| an2 |
| an+a1 |
=(
| a | 2 1 |
| a | 2 2 |
| a | 2 n |
| ||
| a1+a2 |
| ||
| a2+a3 |
| ||
| an+a1 |
| ||
| a1+a2 |
≥(
| a | 2 1 |
| a | 2 2 |
| a | 2 n |
当且仅当a1=a2=…=an=
| 1 |
| n |
| 1 |
| 2 |
点评:本题考查了“乘1法”和基本不等式的性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
在(1+x-
)4的展开式中,常数项是( )
| 1 |
| x2 |
| A、1 | B、13 | C、-11 | D、-2 |
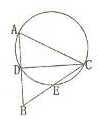 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.