题目内容
已知数列{an}满足a1=1,an+1=
(n∈N),
(1)写出a2、a3、a4、a5值;
(2)由前5项猜想数列{an}通项公式an并证明.
| 2an |
| an+2 |
(1)写出a2、a3、a4、a5值;
(2)由前5项猜想数列{an}通项公式an并证明.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)直接有数列的递推公式进行递推即可得到结论.
(2)根据递推关系,猜想并进行证明即可得到结论.
(2)根据递推关系,猜想并进行证明即可得到结论.
解答:
解:(1)∵a1=1,an+1=
(n∈N),
∴a2=
,a3=
,a4=
,a5=
.
(2)猜想an=
,
由an+1=
(n∈N)得
=
+
,
∴
-
=
,
∴数列{
}是等差数列,
首项
=1,公差d=
,
∴
=
,an=
.
| 2an |
| an+2 |
∴a2=
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 3 |
(2)猜想an=
| 2 |
| n+1 |
由an+1=
| 2an |
| an+2 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 2 |
∴
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 2 |
∴数列{
| 1 |
| an |
首项
| 1 |
| a1 |
| 1 |
| 2 |
∴
| 1 |
| an |
| 2 |
| n+1 |
| n+1 |
| 2 |
点评:本题主要考查递推数列的应用,以及等差数列的证明,考查学生的推理能力.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
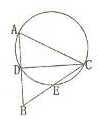 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.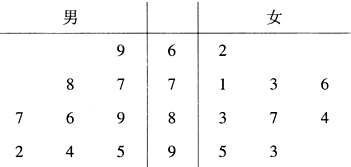 某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.
某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.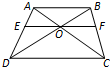 如图,在梯形ABCD中,AB∥CD,AB=3,CD=4.过AC与BD的交点O作EF∥AB,分别交AD,BC于点E,F,则EF=
如图,在梯形ABCD中,AB∥CD,AB=3,CD=4.过AC与BD的交点O作EF∥AB,分别交AD,BC于点E,F,则EF=