题目内容
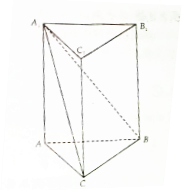 如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=
如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=| 5 |
考点:二面角的平面角及求法
专题:空间角
分析:由勾股定理得AC⊥BC,由线面垂直得BC⊥CC1,从而BC⊥平面ACC1A1,进而BC⊥AC1,由此得∠ACA1是二面角A-BC-A1的平面角,由此能求出当AA1为
时,二面角A-BC-A1为60°.
| 15 |
解答:
解:∵AB=3,BC=2,CA=
,
∴AB2=BC2+CA2,∴AC⊥BC,
∵在直三梭柱ABC-A1B1C1中,CC1⊥平面ABC,
又BC?平面ABC,∴BC⊥CC1,
又AC∩CC1=C,∴BC⊥平面ACC1A1,
又A1C?平面ACC1A1,∴BC⊥AC1,
∴∠ACA1是二面角A-BC-A1的平面角,∴∠ACA1=60°.
∵AA1⊥平面ABC,CA=
,
∴tan∠ACA1=tan60°=
=
,
∴AA1=
•tan60°=
.
∴当AA1为
时,二面角A-BC-A1为60°.
| 5 |
∴AB2=BC2+CA2,∴AC⊥BC,
∵在直三梭柱ABC-A1B1C1中,CC1⊥平面ABC,
又BC?平面ABC,∴BC⊥CC1,
又AC∩CC1=C,∴BC⊥平面ACC1A1,
又A1C?平面ACC1A1,∴BC⊥AC1,
∴∠ACA1是二面角A-BC-A1的平面角,∴∠ACA1=60°.
∵AA1⊥平面ABC,CA=
| 5 |
∴tan∠ACA1=tan60°=
| AA1 |
| CA |
| AA1 | ||
|
∴AA1=
| 5 |
| 15 |
∴当AA1为
| 15 |
点评:本题考查满足条件的线段长的求法,涉及到勾股定理、线面垂直、二面角、三角函数等知识点的合理运用,是中档题.

练习册系列答案
相关题目
已知等比数列{an}的各项均为正数,且公比q≠1,若a2、
a3、a1成等差数列,则公比q=( )
| 1 |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
过双曲线
-
=1(a>0,b>0)的右焦点F作垂直于x轴的直线交双曲线于A,B两点,左顶点C在以AB为直径的圆外,则离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(2,+∞) | ||
| B、(1,2) | ||
C、(
| ||
D、(1,
|
某程序框图如图所示,若该程序运行后输出的值是
,则①处应填( )

| 3 |
| 4 |

| A、k<3 | B、k<4 |
| C、k>3 | D、k>4 |
已知sinα=x,cosβ=y,cos(α+β)=-
,且α,β∈(0,
),则y与x的函数关系为( )
| 11 |
| 14 |
| π |
| 2 |
A、y=-
| ||||||||||
B、y=-
| ||||||||||
C、y=-
| ||||||||||
D、y=-
|