题目内容
已知sinα=x,cosβ=y,cos(α+β)=-
,且α,β∈(0,
),则y与x的函数关系为( )
| 11 |
| 14 |
| π |
| 2 |
A、y=-
| ||||||||||
B、y=-
| ||||||||||
C、y=-
| ||||||||||
D、y=-
|
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由题意和平方关系求出sin(α+β)、cosα,再由两角差的余弦公式求出cosβ,即可得到y与x的函数关系,并求出函数的定义域.
解答:
解:因为cos(α+β)=-
<0,且α,β∈(0,
),
所以
<α+β<π,则sin(α+β)=
=
,
因为sinα=x,α∈(0,
),
所以cosα=
=
(0<x<1),
则y=cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-
×
+
x(0<x<1),
故选:B.
| 11 |
| 14 |
| π |
| 2 |
所以
| π |
| 2 |
| 1-cos2(α+β) |
5
| ||
| 14 |
因为sinα=x,α∈(0,
| π |
| 2 |
所以cosα=
| 1-sin2α |
| 1-x2 |
则y=cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-
| 11 |
| 14 |
| 1-x2 |
5
| ||
| 14 |
故选:B.
点评:本题考查两角差的余弦公式,平方关系,三角函数值的符号,注意角之间的关系,以及函数的定义域.

练习册系列答案
相关题目
在△ABC中,a=2,b=2
,B=45°,则A等于( )
| 2 |
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
计算机执行如图的程序段后,输出的结果是( )


| A、1 | B、2 | C、3 | D、-2 |
若圆C:(x-a)2+(y-a-1)2=a2与x,y轴都有公共点,则实数a的取值范围是( )
A、(-
| ||
B、[-
| ||
C、(-1,-
| ||
D、(-∞,-
|
函数f(x)=x2-2(a+1)x+1在区间[2,+∞)上单调递增,则实数a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,2] |
| C、[1,+∞) |
| D、[2,+∞) |
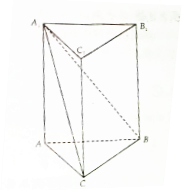 如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=
如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA= 某超市对某商品开展为期两天的抽奖促销活动,第一天的活动方案为:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.
某超市对某商品开展为期两天的抽奖促销活动,第一天的活动方案为:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.