题目内容
当h→0时,
→ .
tan(
| ||||
| h |
考点:变化的快慢与变化率
专题:导数的概念及应用
分析:根据导数的定义,即可求出答案
解答:
解:∵f(x)=tanx=
∴f′(x)=
∴
=f′(
)=
=4,
故答案为:4
| sinx |
| cosx |
∴f′(x)=
| 1 |
| cos2x |
∴
| lim |
| h→0 |
tan(
| ||||
| h |
| π |
| 3 |
| 1 | ||
cos2(
|
故答案为:4
点评:本题考查了导数的定义,属于基础题

练习册系列答案
相关题目
设集合 A={x|2x-1≥5},集合B={x|y=
},则A∩B等于( )
| 3 | ||
|
| A、(3,7) |
| B、[3,7] |
| C、(3,7] |
| D、[3,7) |
命题:“存在x0∈R,sinx0=2”的否定是( )
| A、不存在 x0∈R,sinx0≠2 |
| B、存在 x0∈R,sinx0≠2 |
| C、对任意 x∈R,sinx≠2 |
| D、对任意 x∈R,sinx=2 |
直线(2k2+1)x+(k2-k+1)y=4k2-2k+3与圆(x+1)2+(y+1)2=4的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、不能确定 |
在△ABC中,a=2,b=2
,B=45°,则A等于( )
| 2 |
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
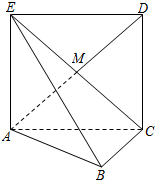 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
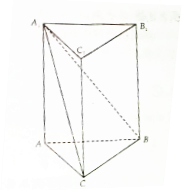 如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=
如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=