题目内容
设函数f（x）=log2（x+1），如果f（x0）＜1，求x0的取值范围．
考点：复合函数的单调性
专题：函数的性质及应用
分析：根据对数函数的性质解对数不等式即可．
解答：
解：∵f（x0）＜1，
∴log2（x0+1）＜1=log22，
∴
，
∴-1＜x0＜1．
即x0的取值范围是（-1，1）．
∴log2（x0+1）＜1=log22，
∴
|
∴-1＜x0＜1．
即x0的取值范围是（-1，1）．
点评：本题主要考查不等式的求解，根据对数函数的单调性的性质是解决本题的关键．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ）+b（A＞0，ω＞0，|φ|＜等差数列{an}中，已知a1=3，a3+a6=7，则a8等于（ ）
| A、4 | B、5 | C、6 | D、7 |
设集合 A={x|2x-1≥5}，集合B={x|y=
}，则A∩B等于（ ）
| 3 | ||
|
| A、（3，7） |
| B、[3，7] |
| C、（3，7] |
| D、[3，7） |
命题：“存在x0∈R，sinx0=2”的否定是（ ）
| A、不存在 x0∈R，sinx0≠2 |
| B、存在 x0∈R，sinx0≠2 |
| C、对任意 x∈R，sinx≠2 |
| D、对任意 x∈R，sinx=2 |
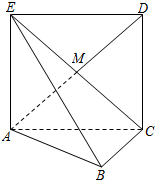如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．
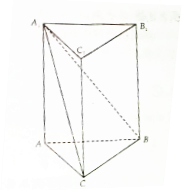如图，在直三梭柱ABC-A1B1C1中，AB=3，BC=2，CA=