题目内容
已知等比数列{an}的各项均为正数,且公比q≠1,若a2、
a3、a1成等差数列,则公比q=( )
| 1 |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:由题意和等差中项的性质列出方程,再由等比数列的通项公式化简,再结合题意求出q的值.
解答:
解:因为a2、
a3、a1成等差数列,
所以2×
a3=a1+a2,则a3=a1+a2,
因为等比数列{an}的各项均为正数,且公比q≠1,
所以a1q2=a1+a1q,化简得q2-q-1=0,
解得q=
或q=
(舍去),
故选:D.
| 1 |
| 2 |
所以2×
| 1 |
| 2 |
因为等比数列{an}的各项均为正数,且公比q≠1,
所以a1q2=a1+a1q,化简得q2-q-1=0,
解得q=
1+
| ||
| 2 |
1-
| ||
| 2 |
故选:D.
点评:本题考查等比数列的通项公式,以及等差中项的性质,属于基础题.

练习册系列答案
相关题目
已知命题p:无穷数列{an}的前n项和为Sn,若{an}是等差数列,则点(n,Sn)在同一条抛物线上;命题q:若实数m>1,则mx2+2(m-2)x+1>0的解集为R,对于命题p的逆否命题s与命题q的逆命题r,下列判断正确的是( )
| A、s是假命题,r是真命题 |
| B、s是真命题,r假命题 |
| C、s是假命题,r是假命题 |
| D、s是真命题,r是真命题 |
等差数列{an}中,已知a1=3,a3+a6=7,则a8等于( )
| A、4 | B、5 | C、6 | D、7 |
设集合 A={x|2x-1≥5},集合B={x|y=
},则A∩B等于( )
| 3 | ||
|
| A、(3,7) |
| B、[3,7] |
| C、(3,7] |
| D、[3,7) |
 已知函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<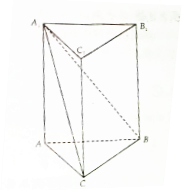 如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=
如图,在直三梭柱ABC-A1B1C1中,AB=3,BC=2,CA=