题目内容
已知a＞b，求证：a3-b3＞ab（a-b）．
考点：不等式的证明
专题：推理和证明
分析：利用作差法，以及立方差公式，即可证明结论；
解答：
证明：a3-b3-ab（a-b）=（a-b）（a2+b2+ab-ab）
=（a-b）（a2+b2）
∵a＞b，∴a-b＞0，a2+b2＞0，
∴（a-b）（a2+b2）＞0．
可得：a3-b3-ab（a-b）＞0．
∴a3-b3＞ab（a-b）．
=（a-b）（a2+b2）
∵a＞b，∴a-b＞0，a2+b2＞0，
∴（a-b）（a2+b2）＞0．
可得：a3-b3-ab（a-b）＞0．
∴a3-b3＞ab（a-b）．
点评：本题考查不等式的证明，考查学生分析解决问题的能力，难度中等．
练习册系列答案
名校课堂系列答案
相关题目
已知命题p：无穷数列{an}的前n项和为Sn，若{an}是等差数列，则点（n，Sn）在同一条抛物线上；命题q：若实数m＞1，则mx2+2（m-2）x+1＞0的解集为R，对于命题p的逆否命题s与命题q的逆命题r，下列判断正确的是（ ）
| A、s是假命题，r是真命题 |
| B、s是真命题，r假命题 |
| C、s是假命题，r是假命题 |
| D、s是真命题，r是真命题 |
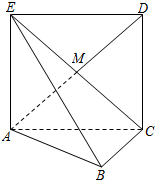如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．
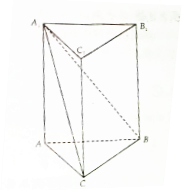如图，在直三梭柱ABC-A1B1C1中，AB=3，BC=2，CA=