题目内容
设f(x)为二次函数,且f(1)=1,f(x+1)-f(x)=-4x+1.
(1)求f(x)的解析式;
(2)设g(x)=f(x)-x-a,若函数g(x)在实数R上没有零点,求a的取值范围.
(1)求f(x)的解析式;
(2)设g(x)=f(x)-x-a,若函数g(x)在实数R上没有零点,求a的取值范围.
考点:抽象函数及其应用,函数的零点
专题:函数的性质及应用
分析:(1)用待定系数法,设出f(x)的解析式,f(x+1)-f(x)=-4x+1中,求出系数即可.
(2)可求得g(x)=-2x2+2x-a,g(x)在实数R上没有零点,?△=4-8a<0,从而可求得a的取值范围
(2)可求得g(x)=-2x2+2x-a,g(x)在实数R上没有零点,?△=4-8a<0,从而可求得a的取值范围
解答:
解:(1)设f(x)=ax2+bx+c(a≠0)
则f(x+1)-f(x)=2ax+a+b
所以2ax+a+b=1-4x对一切x∈R成立.故
所以
,
又因为f(1)=1,所以a+b+c=1,所以c=0.
故f(x)=-2x2+3x
(2)g(x)=f(x)-x-a=-2x2+2x-a,
函数g(x)在实数R上没有零点,则函数图象与x轴没有交点
故△=4-8a<0,
解之得a>
则f(x+1)-f(x)=2ax+a+b
所以2ax+a+b=1-4x对一切x∈R成立.故
|
所以
|
又因为f(1)=1,所以a+b+c=1,所以c=0.
故f(x)=-2x2+3x
(2)g(x)=f(x)-x-a=-2x2+2x-a,
函数g(x)在实数R上没有零点,则函数图象与x轴没有交点
故△=4-8a<0,
解之得a>
| 1 |
| 2 |
点评:本题考查求解函数解析式及一元二次方程的根的分布与系数的关系,着重考查待定系数法,考查二次函数零点,属于中档题.

练习册系列答案
相关题目
关于x的不等式sin2x+acosx-a2≤1+cosx对一切x∈R恒成立,则实数a的取值范围为( )
A、(-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|
已知函数f(x)=
是定义域上的单调减函数,则a的取值范围是( )
|
| A、(1,+∞) | ||||
| B、[2,+∞) | ||||
| C、(1,2) | ||||
D、[
|
函数f(x)=
,若f(2)+f(α)=e+1,则α的所有可能值为( )
|
| A、1 | ||||
B、-
| ||||
C、1或-
| ||||
D、1或
|
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是棱BC上的一点,则三棱锥D1-B1C1E的体积等于( )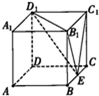

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
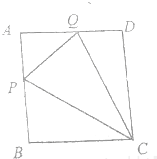 如图,正方形ABCD的边长为1,点P,Q分别在边AB,AD上,且PQ=1,设AP+AQ=x,记△CPQ的面积函数为S=f(x).
如图,正方形ABCD的边长为1,点P,Q分别在边AB,AD上,且PQ=1,设AP+AQ=x,记△CPQ的面积函数为S=f(x).