题目内容
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(Ⅰ)求理科组恰好记4分的概率?
(Ⅱ)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 4 | 4 | 3 | 1 |
(Ⅰ)求理科组恰好记4分的概率?
(Ⅱ)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(I)要求被选出的4人中理科组、文科组的学生都有共有:
+
+
.其中“理科组恰好记4分”的选法有两种情况:从理科组中选取2男1女,再从文科组中任选1人,可有
方法;另一种是从理科组中选取2女,再从文科组中任选2人,可有
方法.根据互斥事件的概率计算公式与古典概型的概率计算公式即可得出.
(II)由题意可得ξ=0,1,2,3.P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=4)=
=
,即可得出分布列与数学期望.
| ∁ | 1 8 |
| ∁ | 3 4 |
| ∁ | 2 8 |
| ∁ | 2 4 |
| ∁ | 3 8 |
| ∁ | 1 4 |
| ∁ | 2 4 |
| ∁ | 1 4 |
| ∁ | 1 4 |
| ∁ | 2 4 |
| ∁ | 2 4 |
(II)由题意可得ξ=0,1,2,3.P(ξ=0)=
| ||||
| 424 |
| 56 |
| 424 |
| ||||
| 424 |
| 252 |
| 424 |
| ||||
| 424 |
| 108 |
| 424 |
| ||||
| 424 |
| 8 |
| 424 |
解答:
解:(I)要求被选出的4人中理科组、文科组的学生都有共有:
+
+
=424.
其中“理科组恰好记4分”的选法有两种情况:从理科组中选取2男1女,再从文科组中任选1人,可有
方法;另一种是从理科组中选取2女,再从文科组中任选2人,可有
方法.
∴P=
=
.
(II)由题意可得ξ=0,1,2,3.P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=4)=
=
,
由题意可得ξ=0,1,2,3.其分布列为:
ξ的数学期望Eξ=0×
+1×
+2×
+3×
=
.
| ∁ | 1 8 |
| ∁ | 3 4 |
| ∁ | 2 8 |
| ∁ | 2 4 |
| ∁ | 3 8 |
| ∁ | 1 4 |
其中“理科组恰好记4分”的选法有两种情况:从理科组中选取2男1女,再从文科组中任选1人,可有
| ∁ | 2 4 |
| ∁ | 1 4 |
| ∁ | 1 4 |
| ∁ | 2 4 |
| ∁ | 2 4 |
∴P=
| 96+36 |
| 424 |
| 33 |
| 106 |
(II)由题意可得ξ=0,1,2,3.P(ξ=0)=
| ||||
| 424 |
| 56 |
| 424 |
| ||||
| 424 |
| 252 |
| 424 |
| ||||
| 424 |
| 108 |
| 424 |
| ||||
| 424 |
| 8 |
| 424 |
由题意可得ξ=0,1,2,3.其分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P(ξ) |
|
|
|
|
| 56 |
| 424 |
| 252 |
| 424 |
| 108 |
| 424 |
| 8 |
| 424 |
| 123 |
| 106 |
点评:本题考查了互斥事件的概率计算公式与古典概型的概率计算公式、随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
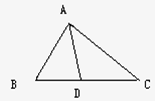
如图,在△ABC中,AB=3,AC=4,BC=5,AD平分∠BAC,则BD的值为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
是定义域上的单调减函数,则a的取值范围是( )
|
| A、(1,+∞) | ||||
| B、[2,+∞) | ||||
| C、(1,2) | ||||
D、[
|