题目内容

若实数x，y满足不等式组
2-x≤0
y≤x
2x+y+k≤0
（其中k为常数），若z=x+3y的最大值为5，则k的值等于
 
．
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z=x+3y的最大值为5，确定最优解，建立方程，即可得到结论．
解答： 解：作出不等式组对应的平面区域如图：
由z=x+3y的最大值为5得，5=x+3y，
即y=-
1
3
x+
5
3
，则对应的平面区域在直线y=-
1
3
x+
5
3
的下方，
由
x+3y=5
x=2
，解得
x=2
y=1
，
即A（2，1），此时点A也在直线2x+y+k=0上，
即4+1+k=0，
解得k=-5．
故答案为：-5
点评：本题主要考查线性规划的逆用，利用数形结合先确定最优解是解决本题的关键．
练习册系列答案
相关题目
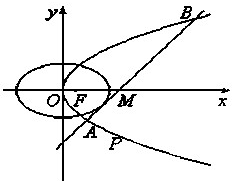如图所示，已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A，B两点．
（Ⅰ）写出抛物线C2的标准方程；
（Ⅱ）求证：以AB为直径的圆过原点；
（Ⅲ）若坐标原点关于直线l的对称点P在抛物线C2上，直线l与椭圆C1相切，求椭圆C1的标准方程．
已知双曲线C：
x2
a2
-
y2
b2
=1的焦距为3
2
，其中一条渐近线的方程为x-
2
y=0．以双曲线C的实轴为长轴，虚轴为短轴的椭圆记为E，过原点O的动直线与椭圆E交于A、B两点．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若点P为椭圆的左顶点，
PG
=2
GO
，求|
GA
|2+|
GB
|2的取值范围；
（Ⅲ）若点P满足|PA|=|PB|，求证
1
|OA|2
+
1
|OB|2
+
2
|OP|2
为定值．
已知双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的焦距为2
7
，其一条渐近线的倾斜角为θ，且tanθ=
3
2
．以双曲线C的实轴为长轴，虚轴为短轴的椭圆记为E．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设点A是椭圆E的左顶点，P、Q为椭圆E上异于点A的两动点，若直线AP、AQ的斜率之积为-
1
4
，问直线PQ是否恒过定点？若恒过定点，求出该点坐标；若不恒过定点，说明理由．
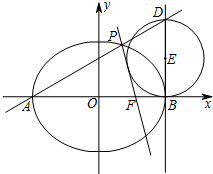已知椭圆C的中心在坐标原点，右焦点为F（1，0），A、B是椭圆C的左、右顶点，P是椭圆C上异于A、B的动点，且△APB面积的最大值为2
3
．
（1）求椭圆C的方程；
（2）直线AP与直线x=2交于点D，证明：以BD为直径的圆与直线PF相切．
已知直线l：
x=t
y=t-2
(t为参数)与曲线C：
x=2cosθ
y=2sinθ
(θ为参数）交于A、B两点，则|AB|=
 
．
若方程|logax|=||x-3|-1|有三解，则实数a的取值范围是
 
．
已知实数x，y满足
y≤x
x+y≤1
y≥-1
，则x+2y的最大值是
 
．
定义在R上的奇函数f（x）满足f（x-2）=-f（x），且在[0，1]上是增函数，则有（　　）
A、f(
1
4
)＜f(-
1
4
)＜f(
3
2
)
B、f(-
1
4
)＜f(
1
4
)＜f(
3
2
)
C、f(
1
4
)＜f(
3
2
)＜f(-
1
4
)
D、f(-
1
4
)＜f(
3
2
)＜f(
1
4
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网