��Ŀ����
15��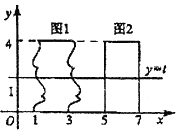 �ҹ��ϱ���ʱ������ѧ���敜�������ļ���ԭ�����镜ԭ�����������Ƽ�ͬ����������족�����ơ����Ǹߣ����ݡ����������˼�ǣ�������ȸߵļ�������ͬ�ߴ��õ���������IJ������ȣ���ô������������������ȣ�����敜ԭ������ͼ��ʾ����ƽ��ֱ������ϵ�У�ͼ1��һ����״������ķ��ͼ�Σ�ͼ2��һ�����Σ��ҵ�ʵ��tȡ[0��4]�ϵ�����ֵʱ��ֱ��y=t��ͼ1��ͼ2���صõ��߶�ʼ����ȣ���ͼ1�����Ϊ8��
�ҹ��ϱ���ʱ������ѧ���敜�������ļ���ԭ�����镜ԭ�����������Ƽ�ͬ����������족�����ơ����Ǹߣ����ݡ����������˼�ǣ�������ȸߵļ�������ͬ�ߴ��õ���������IJ������ȣ���ô������������������ȣ�����敜ԭ������ͼ��ʾ����ƽ��ֱ������ϵ�У�ͼ1��һ����״������ķ��ͼ�Σ�ͼ2��һ�����Σ��ҵ�ʵ��tȡ[0��4]�ϵ�����ֵʱ��ֱ��y=t��ͼ1��ͼ2���صõ��߶�ʼ����ȣ���ͼ1�����Ϊ8��
���� �����敜ԭ�����ɵ�ͼ1�����=���ε���������ɵó����ۣ�
��� �⣺�����敜ԭ�����ɵ�ͼ1�����Ϊ4��2=8��
�ʴ�Ϊ8��
���� ���⿼���˾��ε������ʽ����������ѧ���ռ���������������㼼�ܣ�

��ϰ��ϵ�д�
�����Ŀ
11����a=lg$\frac{2}{3}$��b=lg$\frac{2}{5}$��c=lg$\frac{3}{2}$��������
| A�� | a��c��b | B�� | b��c��a | C�� | c��b��a | D�� | c��a��b |
3����֪����A={x|��x-1����3-x����0}��B={x|-2��x��2}����A��B=��������
| A�� | [-2��1�� | B�� | ��1��2] | C�� | [-2��-1�� | D�� | ��-1��2] |
7�����������У���ȷ���ǣ�������
| A�� | x3•x2=x5 | B�� | x+x2=x3 | C�� | 2x3��x2=x | D�� | ��$\frac{x}{2}$��3=$\frac{{x}^{3}}{2}$ |
4����ijʵ���45��ͬѧ�������ȡ5��ͬѧ�μӡ���ս�������������������ȷ����5��ͬѧ���ֽ��������ժ¼�������£�
�����������һ�еĵ�5�к͵�6�����ֿ�ʼ����������ѡȡ�������֣���ѡ���ĵ�5��ͬѧ�ı��Ϊ��������
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A�� | 23 | B�� | 37 | C�� | 35 | D�� | 17 |
5����֪F1��F2�ֱ���˫����C��$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0�������ҽ��㣬G��˫����C��һ�㣬������|GF1|-7|GF2|=0����C������һ���Ľ����ߵ�б�ʵ�ȡֵ��Χ�ǣ�������
| A�� | ��0��$\frac{\sqrt{7}}{3}$] | B�� | ��0��$\frac{\sqrt{5}}{2}$] | C�� | ��$\sqrt{2}$��$\frac{5}{3}$] | D�� | ��$\sqrt{2}$��$\frac{\sqrt{13}}{3}$] |
 ��ͼ��������PDC���ڵ�ƽ���볤����ABCD���ڵ�ƽ�洹ֱ��
��ͼ��������PDC���ڵ�ƽ���볤����ABCD���ڵ�ƽ�洹ֱ��