题目内容
10.已知函数f(x)=ex-k-x,(x∈R).(1)当k=0时,若函数f(x)≥m在R上恒成立,求实数m的取值范围;
(2)试判断当k>1时,函数f(x)在(k,2k)内是否存在两点;若存在,求零点个数.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,得到函数f(x)的最小值,从而求出m的范围即可;
(2)求出f(x)的导数,计算f(k),f(2k)的值,根据函数f(x)的单调性,令h(k)=ek-2k,结合零点存在定理判断即可.
解答 解:(1)当k=0时,f(x)=ex-x,f'(x)=ex-1,
令f'(x)=0,得x=0,当x<0时,f'(x)<0;当x>0时,f'(x)>0,
∴f(x)在(-∞,0)上单调递减,在[0,+∞)上单调递增.
∴f(x)min=f(0)=1,∴m≤1,
∴实数m的取值范围是(-∞,1].
(2)当k>1时,f(x)=ex-k-x,f'(x)=ex-k-1>0在(k,2k)上恒成立.
∴f(x)在(k,2k)上单调递增,
又f(k)=ek-k-k=1-k<0,f(2k)=e2k-k-2k=ek-2k,
令h(k)=ek-2k,
∵h'(k)=ek-2>0,∴h(k)在k>1时单调递增,
∴h(k)>e-2>0,即f(2k)>0,
∴由零点存在定理知,函数f(x)在(k,2k)内存在唯一零点.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道中档题.

练习册系列答案
相关题目
5. 如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )
如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )
 如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )
如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )| A. | p=1 | B. | p=2 | C. | p=$\frac{1}{2}$ | D. | p=$\sqrt{2}$ |
19.为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:
已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
(1)请将上面的列表补充完整;
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论: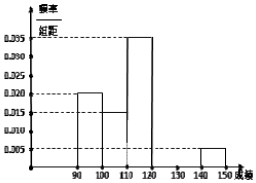 某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.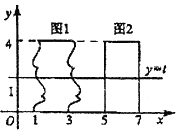 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.