题目内容
定义一种运算a?b=
例如2?3=2,令f(x)=(cos2x+sinx)?
,x∈[0,
],则函数f(x-
)的最大值是( )
|
| 5 |
| 4 |
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
考点:函数的最值及其几何意义
专题:计算题,新定义,函数的性质及应用
分析:先根据新定义,确定函数解析式,再化简函数f(x-
),利用配方法,即可求得最大值.
| π |
| 2 |
解答:
解:由于cos2x+sinx=-sin2x+sinx+1=-(sinx-
)2+
≤
∴f(x)=(cos2x+sinx)?
=cos2x+sinx,
f(x-
)=cos2(x-
)+sin(x-
)=sin2x-cosx=-(cos2x+cosx+
)+1+
=-(cosx+
)2+
∵x-
∈[0,
],∴x∈[
,π],∴f(x-
)≤
故选:A.
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
∴f(x)=(cos2x+sinx)?
| 5 |
| 4 |
f(x-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
∵x-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5 |
| 4 |
故选:A.
点评:本题考查新定义,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知△ABC中,a=7,b=5,c=3,A=120°,则高AD=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若称集合A旳非空真子集的真子集为集合A的“孙子集”,则集合A{A,B,C,D}的“孙子集”有( )
| A、16个 | B、15个 |
| C、11个 | D、10个 |
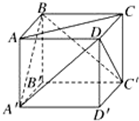 若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )
若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )| A、12对 | B、18对 |
| C、24对 | D、30对 |
 一个正方体的六个面上分别标有A,B,C,D,E,F,如图是正方体的两种不同放置,则与D面相对的面上的字母是
一个正方体的六个面上分别标有A,B,C,D,E,F,如图是正方体的两种不同放置,则与D面相对的面上的字母是