题目内容
(1)在(x-
)2004的二项式中,含x的奇次幂的项之和为S,当x=
时,求S.
(2)已知(x2-
)n的展开式中第三项与第五项的系数之比为-
,求展开式中常数项.
(3)若多项式x2+x10=a0+a1(x+1)+…+a9(x+1)9+a10(x+1)10,求a9.
| 2 |
| 2 |
(2)已知(x2-
| i | ||
|
| 3 |
| 14 |
(3)若多项式x2+x10=a0+a1(x+1)+…+a9(x+1)9+a10(x+1)10,求a9.
考点:二项式定理的应用,二项式系数的性质
专题:综合题,二项式定理
分析:(1)利用二项式定理将二项式展开,令x分别取
,-
得到两个等式,两式相减,化简即可求s的值;
(2)利用二项展开式的通项公式求出展开式中第三项与第五项的系数,列出方程求出n;利用二项展开式的通项公式求出第r+1项,令x的指数为0求出常数项;
(3)先求x10的系数,再由a9+C109•a10,可求x9的系数,即可得答案.
| 2 |
| 2 |
(2)利用二项展开式的通项公式求出展开式中第三项与第五项的系数,列出方程求出n;利用二项展开式的通项公式求出第r+1项,令x的指数为0求出常数项;
(3)先求x10的系数,再由a9+C109•a10,可求x9的系数,即可得答案.
解答:
解:(1)设(x-
)2006=a0x2006+a1x2005+…+a2005x+a2006;
则当x=
时,有a0(
)2006+a1(
)2005+…+a2005(
)+a2006=0①,
当x=-
时,有a0(
)2006-a1(
)2005+…-a2005(
)+a2006=23009②,
①-②有a1(
)2005+…+a2005(
)=-23009÷2=-23008;
(2)第三项的系数为-
,第五项的系数为
,由第三项与第五项的系数之比为-
可得n=10,则Tr+1=
(x2)10-r(-
)r=(-i)r
x
,
令40-5r=0,解得r=8,故所求的常数项为(-i)8
=45;
(3)x10的系数为a10,∴a10=1,x9的系数为a9+C109•a10,∴a9+10=0,∴a9=-10.
| 2 |
则当x=
| 2 |
| 2 |
| 2 |
| 2 |
当x=-
| 2 |
| 2 |
| 2 |
| 2 |
①-②有a1(
| 2 |
| 2 |
(2)第三项的系数为-
| C | 2 n |
| C | 4 n |
| 3 |
| 14 |
| C | r 10 |
| i | ||
|
| C | r 10 |
| 40-5r |
| 2 |
令40-5r=0,解得r=8,故所求的常数项为(-i)8
| C | 8 10 |
(3)x10的系数为a10,∴a10=1,x9的系数为a9+C109•a10,∴a9+10=0,∴a9=-10.
点评:本题主要考查二项式定理的运用,二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目
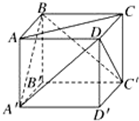 若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )
若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )| A、12对 | B、18对 |
| C、24对 | D、30对 |
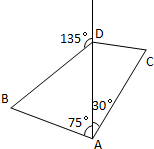 如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距
如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距